Stack (Last-In-First-Out)

graph LR
	ALG(["fas:fa-trophy Stack fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	ARRAY(["fas:fa-check Array #160;"])
    click ARRAY "./list-data-struct-array"

	LL(["fas:fa-check Linked List #160;"])
    click LL "./list-data-struct-linked-list"

	ASY_ANA-->ALG
    ARRAY-->ALG
    LL-->ALG

The stack, aka Last-In-First-Out (LIFO) list or pushdown store, data structure is surprisingly simple yet equally useful. Their primary purpose is to track a linear list of items in last-in-first-out order. As an example, consider a spring loaded stack of plates in a restaurant buffet line¹. The last plate placed on top of the stack is the first plate removed and it’s not possible to remove a plate on the bottom without first removing the plates above it. Likewise, consider browser history: each new address is added to a stack. Pressing the back button removes the newest item from the stack and returns it.

History

The stack concept was employed in many forms long before it had a explicit name. For example, its use in accounting dates back to the 1800s². As applied to computation, the exact origin is difficult to pinpoint. In 1947, Alan Turing described a stack like construct with bury and unbury operations. The earliest known fully formed representation was in a 1959 paper entitled Report on a General Problem-Solving Program by Newell, Shaw, and Simon³. The paper outlined a LIFO structure required to formulate pushdown automata which was a milestone in theoretical computation. However, its use is not sequestered to theory.

Edsger Dijkstra coined the term stack to denote LIFO data in his 1960 paper entitled Recursive Programming⁴. He used stacks to implement recursion in his Algol 60 compiler. The term caught on and is presently ubiquitous. Stacks are quite possibly the most common data structure in use today.

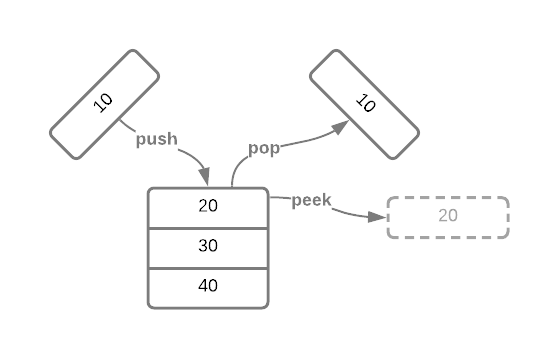
Stacks have three primary operations: push, pop, and peek⁵. They are outlined in the Pseudo Code section, take a minute to read them over. The image below depicts stack operations graphically.

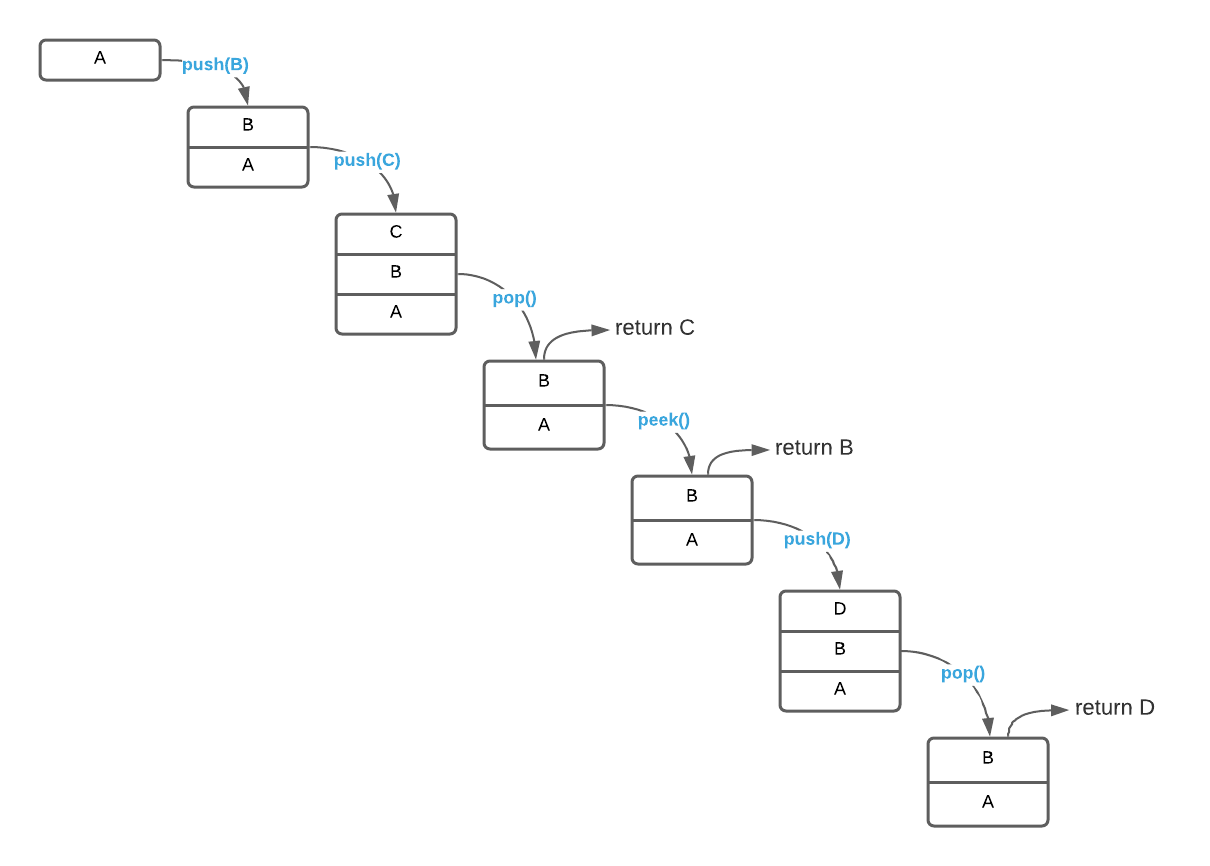
To solidify the concept, consider a stack of character data. The image below depicts a series of operations.

Common Exceptions

No discussion of stacks is complete without mentioning the most popular programming exception ever conceived⁶: stack overflow. An overflow occurs when a push operation exceeds the memory available to a stack data structure. Suppose you have a stack data structure that is only capable of holding five items. In this case, six successive push operations will yield a stack overflow. At the other end of the spectrum is stack underflow. This exception occurs when attempting a pop or peek operation on an empty stack.

Certain stack implementations are more prone to stack overflows than others⁷. Stated differently, some implementations are constrained by a fixed sized while others are not⁸. Regardless, underflow is always a possibility. It’s common to create an is_empty operation to aid in overflow prevention. If is_empty returns true, the consumer knows that a pop will throw an underflow exception.

It’s wise to incorporate these well-known exception types into your own designs. The verbiage will be immediately recognizable by most seasoned programmers. This is something to keep in mind while completing the exercises.

Applications

• Memory Management: Operating systems use a stack for managing memory.
• Syntax Parsing: Compilers use stacks for expression parsing.
• Backtracking: Keep track of tasks so they can be undone if necessary. Think of what happens when you press ctrl+z while using MS Word, or u when using VIM.
• Graph Depth First Search

Pseudo Code

\begin{algorithm}
\caption{Stack Abstract Interface}
\begin{algorithmic}
\REQUIRE value = value to add to the stack
\FUNCTION{push}{value}
    \STATE add value to top of STACK
\ENDFUNCTION
\FUNCTION{pop}{}
    \STATE value $\gets$ top of STACK
    \STATE STACK $\gets$ STACK - value
    \RETURN value
\ENDFUNCTION
\FUNCTION{peek}{}
    \RETURN value at top of stack
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Implementation Details

A Linked List is an ideal data structure for implementing a stack. However, an Array is also a viable option.

Asymptotic Complexity

• Push: $O(1)$
• Pop: $O(1)$
• Peek: $O(1)$

Source Code

Full Repo

Relevant Files:

• stack.h
• stack.c
• stack_test.c

Click here for build and run instructions

Exercises

1. Consult the supplied Pseudo Code to answer this question. With the assumption that you are starting with a well formed empty stack capable of tracking integer values, list the items that exist on the stack after the following operations:
   a. push(55); push(45); peek(); pop(); push(65);
   b. push(1); push(3); push(8);
   c. push(75); push(85); pop(); peek();
   d. push(100); peek(); pop(); push(200); pop(); pop();

   Answers (click to expand)

   1. 65
      55
   2. 8
      3
      1
   3. 75
   4. Stack Underflow

2. Specify detailed pseudo code for a stack implementation using a:
   a. Fixed length array.
   b. Linked list.

   For formatting purposes, the answers to question 2 are located here.

3. Using the programming language of your choice, write a program that accepts a random list of integers, stores them on a stack, and prints them in the reverse order that they were received.