Bellman-Ford Shortest Path

The Bellman-Ford algorithm was discovered by at least three different people independently in the 1950s. These people include Richard E. Bellman, Lester R. Ford, and Alfonso Shimbel. Shimbel’s name was never associated with the algorithm; however, there is some evidence that he was the first to discover it.

The Bellman-Ford algorithm determines the shortest path between a source vertex and all other vertices (typically referred to as the single source shortest path problem). It is a bit slower than Dijkstra’s algorithm; however, it has two added benefits. First, the graph does not have to exist in a single memory space, it can be disbursed (e.g. network of packet routers). The other benefit is that it works with negative edge weights given one caveat: there are no negative cycles. A negative cycle is a cycle where the sum of it’s edge lengths is negative. Consider the image below. The cycle from A to A is $3 + -5 + 4 + -6 = -4$ which constitutes a negative cycle.

Negative Cycle

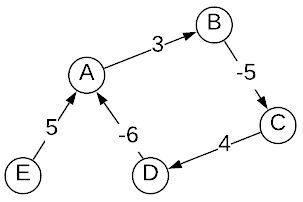
Given the negative cycle depicted above, the path length from E to A is $-\infty$. After traversing from E to A, the path length can be repeatedly reduced by following A’s cycle. This is why the algorithm cannot accommodate negative cycles. One might logically conclude that this limitation can be easily overcome by simply ignoring negative cycles. Unfortunately, discarding the negative cycle is a $NP$-hard problem. In light of these restrictions, the algorithms will either return the shortest path or a message indicating that a negative path exits.

Applications

Internet Routing (It’s interesting is that this algorithm was discovered more than 10 years before ARPANET which was the earliest form of the internet.)
Algorithmic Financial Trading (Detect arbitrage opportunities by identifying negative cycles)

Asymptotic Complexity

$O(mn)$ where $n$ is the number of vertices and $m$ is the number of edges

Pseudo Code

inputs:
    G graph
    v starting vertex

solutions[graph->n + 1][graph->n]

for every v in graph->V:
    solutions[0] = infinity

solutions[0][v] = 0

for 1 to graph->n:
    stable = true
    for v in graph->V:
        shortest = infinity
        for e in v->incoming_edges:
            shortest = min(shortest, solutions[i-1][e->tail] + e->weight)
            
        solutions[i][v] = min(shortest, solutions[i-1][v])

        if solutions[i-1][v] != solutions[i][v]:
            stable = false

     if (stable):
        return solutions[i]

   return "negative cycle detected"

Source Code

Full Repo

Relevant Files:

Click here for build and run instructions