Set Notation

graph LR
    classDef currentPage stroke:#333,stroke-width:4px

	ALG(["fas:fa-trophy Algorithmis fas:fa-trophy "])

	ASY_ANA(["fas:fa-check Asymptotic Analysis#160;"])
    click ASY_ANA "./math-asymptotic-analysis"

    

	MAT_NOT(["fas:fa-check Mathematical Notation#160;"])
    click MAT_NOT "./math-notation"

    

	POL(["fas:fa-check Polynomials #160;"])
    click POL "./math-polynomials"

    

	MAT_FUN(["fas:fa-check Math Functions#160;"])
    click MAT_FUN "./math-functions"

    

	LOG(["fas:fa-check Logarithms#160;"])
    click LOG "./math-logarithms"

    

	COM(["fas:fa-check Combinatorics#160;"])
    click COM "./math-combinatorics"

    

	SET_NOT(["fas:fa-check Set Notation#160;"])
    click SET_NOT "./math-set-notation"

    
      class SET_NOT currentPage
    

	GRA(["fas:fa-check Graphing#160;"])
    click GRA "./math-graphing"

    

	BW(["fas:fa-check Bitwise Logic#160;"])
    click BW "./math-bitwise"

    

	MAT(["fas:fa-check Matrices#160;"])
    click MAT "./math-matrices"

    

	ASY_ANA-->ALG
	BW-->ALG
    MAT-->ALG
    COM & GRA & SET_NOT-->ASY_ANA
    MAT_NOT--> SET_NOT
    POL & LOG--> MAT_FUN
    MAT_FUN--> GRA

Set theory is an absolutely fascinating branch of mathematics. It’s intuitively simple on the surface; however, it’s incredibly deep and has far-reaching implications. “The axioms of set theory imply the existence of a set-theoretic universe so rich that all mathematical objects can be construed as sets”¹. Fortunately or perhaps unfortunately depending on your perspective, the portion of set theory that applies to algorithms is diminutive albeit ubiquitous. This page focuses on the set of concepts (pun intended) that apply to algorithm design and analysis.

This section has an ancillary purpose as it also serves as an introduction to mathematical notation in general. It’s important to become fluent in written math for two reasons. The first is that reading and writing proofs is requisite for algorithm mastery. The second is that it is an efficient medium for communicating dense concepts. The concise symbols that comprise the language of math is far more expressive and precise than natural languages such as English, Spanish, etc…

Those in the software field often struggle with mathematical notation because written math, while far more precise than natural language, is not nearly as Draconian as typical programming languages. Miswritten syntax in math has no impact (assuming it’s still comprehensible). A syntax error while programming results in a compiler error. Remember that mathematical notation is a matter of convention and authors tend to interpret the convention loosely. There are several correct ways to write the same thing. For instance, $A^\prime$, $A^\complement$, and $A^\sim$ are all equivalent. What’s worse, it’s also common to see the same symbol with a different meaning depending on the context. For instance, the symbol $\Sigma$ denotes a summation; however, it’s not uncommon to define it to be an arbitrary variable. Deriving meaning from mathematical notation takes practice. Do not be discouraged if it isn’t painfully obvious at first. Keeping all this in mind, understand that every attempt is made to showcase the most common representations; however, it’s highly likely that you will encounter variations.

PRO TIP: Bookmark this page in the event that you encounter a symbol you don’t recognize.

History

Georg Cantor introduced set theory in his 1874 paper entitled On a Property of the Collection of All Real Algebraic Numbers. Although controversial at the time, set theory was a major breakthrough in mathematics. Georg’s paper essentially proved that there are multiple sizes of infinity. The concept is so powerful that it is used as a foundation for all of mathematics.

Set theory sustained a crippling blow in the early 1900s when Bertrand Russell formulated what is know as Russell’s Paradox. Mr. Russell wrote about it in a book that he co-authored with Alfred North-Whitehead entitled Principia Mathmatica². The book was published in 1903. In a nutshell, a logical inconstancy arises when trying to formulate the set of all sets that are not members of themselves. The said set is only a member of itself if it’s not a member of itself. Luckily, set theory was so incredibly useful that it was not abandoned. Ernet Zermelo and Abraham Fraenkel reformulated set theory to alleviate the paradox. Georg’s original theory is now referred to as naive set theory and the more complete theory is called axiomatic or Zermelo-Fraenkel set theory.

In the domain of computer science, naive set theory is more than adequate. All of the relevant concept are covered here. Although the wider topic of set theory is not directly applicable to algorithms, it’s an absolutely fascinating topic that anyone will enjoy exploring.

What is a Set?

Set theory concerns grouping objects, known as members or elements, into well-defined unordered sets. All the items within a set are unique; that is, duplicates are not allowed. This is a familiar concept as it’s taught in grade school. As an example, consider the Kardashians; each family member (Kim, Khloe, Kourtney, Rob, etc…) is an element in the Kardashian set. A more formal example is the classification of the animal kingdom into sets known as phyla, class, order, family, and genus. Before continuing on, take a minute and try to identify a few well-defined sets.

Sets are depicted as objects inside curly braces and are denoted by capital letters. For instance, \(A=\{1,2,3\}\) is the mathematical representation of the set $A$ with the members $1$, $2$, and $3$. Sets can contain other sets such as \(B=\{\{1,2\},\{2,4\}\}\). The symbol $\emptyset$, alternatively \(\{\}\), represents the empty set (set with no objects). Conversely, $\U$ is the universe (aka universal set or universe of discourse) which contains all possible elements in an area of interest. The number of items included in a set, represented by surrounding vertical bars, is called the cardinality³ of the set. $\vert A \vert$ means the “cardinality of $A$”. As $A$ is defined in this paragraph, $\vert A \vert=3$.

Summary

Symbol	Description
\(\{1, 2\}\)	Set containing the members $1$ and $2$
$\emptyset$	Empty set — set with no members
$\U$	Universe — set with all members in the area of interest
$\vert A\vert$	Cardinality (number of items in set) of set $A$

$\U$ Number Sets

It’s common to constrain the types of numbers that an algorithm accepts or generates. Set theory defines several sets of numbers based on their properties. See the table below.

Symbol	Name	Description
$\N$	Natural (aka Counting)	All positive whole numbers including 04
$\Z$5	Integers	$\N$ + negative whole numbers
$\Q$	Rational (Quotient)	$\Z$ + numbers representable as fractions such as $\frac{1}{2}$ or $\frac{3}{4}$
$\R$	Real	$\Q$ + irrational numbers including algebraic numbers (e.g. $\sqrt{2}$) and transcendental numbers (e.g. $\pi$ and $e$)

There are many more well-defined numbers sets⁶; however, the above is sufficient for the purposes at hand. The astute reader may have noticed that each successive set encompasses the previous set. This is by design. The Venn diagram below represents the relationship between the number sets.

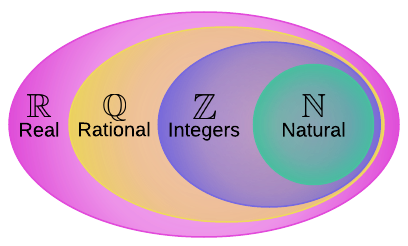
Another way to express the diagram above is $\N \subset \Z \subset \Q \subset \R$. The next section elaborates on the $\subset$ symbol.

Related Sets

When a set in comprised of elements from a larger set, it is said to be a subset of that set. From the opposite perspective, a larger set that contains all items in a smaller set is a superset. This is depicted graphically below.

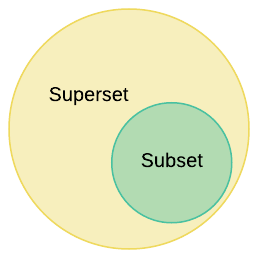
The $\subset$ symbol indicates a subset relationship and a $\supset$ symbol denotes a superset relationship as shown in mathematical notation below.

\[A=\{1,2,3\}, B=\{1,2,3,4,5\}\] \[A \subset B, B \supset A\]

Strictly speaking, what’s shown above are proper subsets and supersets. The proper distinction means that the subset is not equal to the superset or vice versa. If the possibility exists that the two sets are equals the symbols $\subseteq$ and $\supseteq$ are used as shown below.

\[A=\{1,2,3,4,5\}, B=\{1,2,3,4,5\}\] \[A \subseteq B, B \supseteq A\]

Stated differently, if $\alpha \subseteq \sigma$ then $\sigma$ contains every element that $\alpha$ contains. If $\alpha \subset \sigma$ then $\sigma$ contains every element that $\alpha$ contains and some additional elements. Although it may seem like a pedantic distinction, it’s valuable in practice.

There is also convenient notation for indicating the lack of a relationship. A $/$ through a symbol negates the relationship. Each of the set symbols shown above has an equivalent negated symbol: $\not\subseteq$, $\not\subset$, $\not\supseteq$, and $\not\supset$. See the mathematical statements below.

\[A=\{1,2,3,4,5\}, B=\{6,7,8,9,10\}\] \[A \not\subset B, B \not\supset A\]

A final important relationship is a set’s complement. The complement of a set is all the items in $\U$ that are not in the set. See the image below. The complement of $A$ in mathematical notation is $A^\prime$. It is also common to see $A^\complement$, $\overline{A}$, or $A^\sim$.

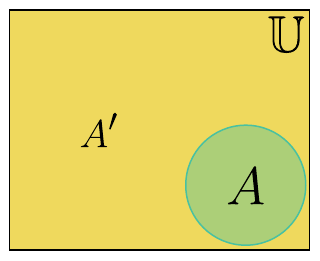
As is evident by now, there are many symbols. Don’t be alarmed if they are difficult to remember. They are all summarized below for easy referral.

Summary

Symbol	Name	Example	Negation
$\subseteq$	Subset	\(\{1,2,3\} \subseteq \{1,2,3\}\)	$\not\subseteq$
$\subset$	Proper Subset	\(\{1,2\} \subset \{1,2,3\}\)	$\not\subset$
$\supseteq$	Superset	\(\{1,2,3\} \supseteq \{1,2,3\}\)	$\not\supseteq$
$\supset$	Proper Superset	\(\{1,2,3\} \supset \{1,2\}\)	$\not\supset$
$^\prime$	Complement	\(\U=\{1,2,3\}, A=\{1,2\}, A^\prime=\{3\}\)

Building a Set

The elements belonging to a well-defined set share certain properties as defined by the set. This section describes the notation for describing those properties. The first task is to denote set membership. The symbol $\in$, read as “is a member of”, indicates that an element belongs to a set. For instance, $\sigma \in A$ indicates that the element $\sigma$ is included in the set $A$. Read aloud, it says “$\sigma$ is a member of $A$”. Contrarily, the symbol $\notin$ indicates the opposite. $\sigma \notin A$ is read as “$\sigma$ is not a member of $A$”. See the examples below.

\[1 \in \{1, 2\}\] \[3 \notin \{1, 2\}\]

As has already been demonstrated, one way of defining a set is to list all the members inside \(\{\}\)s (e.g. \(A=\{1,2,3\}\)). Inconveniently, many sets are so large that listing all the elements isn’t a possibility. One way to overcome this limitation is to use a $\ldots$ symbol to denote a sequence. For instance, the notation for a set of whole numbers between $1$ and $100$ is:

\[\{1,2,3,\ldots,100\}\]

Omitting the ending or beginning number indicates that the sequence extends through infinity as illustrated below.

\[\N = \{0,1,2,\dots\}\] \[\Z = \{...,0,1,2,\dots\}\]

Strictly speaking, the remaining symbols in this section are predicate logic symbols rather than set notation. However, this is a pedantic distinction. It makes sense to introduce them here because they are often seen together.

Not all sets conform to a sequence. In these cases, the $\vert$ symbol combined with a predicate suffices. $\vert$ is the such as symbol. A predicate is an expression that accepts a single argument and returns a true or false value. Any value that satisfies the predicate (yields a true result) is a member of the set. This is best demonstrated with an example. The statement below reads: the set of all elements from the real numbers set such that $x \lt 0$. Stated differently, the set of all negative real numbers.

\[\{x \in \R \vert x \lt 0\}\]

It’s also possible to express set assertions in mathematical notation. The $\forall$ symbol, read as for all, represents all members in a set. The following statement reads: for all members in the $\N$ set, the member is $\geq 0$. Alternatively, every member in $\N$ is greater than or equal to zero.

\[\forall x \in \N, x \geq 0\]

Another common symbol is $\exists$ which is known as the existential qualification. It asserts that at least one item exists that satisfies the specified predicate. The statement below reads, there exists at least one element in $\N$ that is even.

\[\exists x \in \N,x \bmod 2=0\]

The notation introduced up to this point concerns defining sets and their elements. The following section outlines set operations.

Summary

Symbol	Name	Example
$\in$	is a member of	\(1 \in \{1,2,3\}\)
$\notin$	is not a member of	\(4 \notin \{1,2,3\}\)
$\ldots$	sequence	\(\N = \{0,1,2,\dots\}\)
$\vert$	such that	\(\{x \vert x > 0\} = \{1,2,3,...\}\)
$\forall$	for all	\(\forall x \in \{2,4,6,8\}, x \bmod 2=0\)
$\exists$	there exists	\(\exists x \in \{1,2,3,4\},x \bmod 2=0\)

Set Operations

Similar to numbers, sets support basic arithmetic operations. This section outlines five such operations. The first is the set union represented by the $\cup$ symbol. A result of a union operation on two sets is a new set with all the distinct elements from both sets combined. Notice the word distinct; if an item exists in both sets, it’s not duplicated. See the example below.

\[\{a,b,c,d,e\} \cup \{c,d,e,f,g,h\} = \{a,b,c,d,e,f,g,h\}\]

The $\cap$ symbol represents a set intersection. The intersection of two sets is the items that both sets have in common as shown below.

\[\{a,b,c,d,e\} \cap \{c,d,e,f,g,h\} = \{c,d,e\}\]

Taking the difference of two sets works the same way as it does with numbers. Subtracting $A$ from $B$ results in a set with all the items in $B$ that are not in $A$. The set difference symbol ($-$) is even the same as the symbol used for subtracting numbers. See the example below.

\[\{a,b,c,d,e\} - \{a,b,c\} = \{d,e\}\]

The three operations outlined above are fairly innocuous. However, the multiplication operation can seem a bit strange on first inspection. Multiplying two sets generates the Cartesian product of the sets. The Cartesian product is the set of ordered pairs (2-tuples⁷) with the first element from the first set and the second from the second set. This is easier to explain using set builder notation as shown below.

\[A \times B = \{(a,b) \vert a \in A \; \text{and} \; b \in B\}\]

Stated differently, the Cartesian product of $A$ and $B$ is the set of all ordered pairs $(a, b)$ where $a$ is in $A$ and $b$ is in $B$. See the graphical depiction below.

\[\green{\{e,f,g\}} \times \blue{\{a,b,c\}} = \begin{array}{c|c} \green{ \quad\;\begin{matrix} \{a,\quad & b,\quad & c\} \end{matrix} } \\ \blue{ \begin{matrix} \{e,\\ f,\\ g\} \end{matrix} } \left[\ \begin{matrix} (\blue{e},\green{a}) & (\blue{e},\green{b}) & (\blue{e},\green{c})\\ (\blue{f},\green{a}) & (\blue{f},\green{b}) & (\blue{f},\green{c})\\ (\blue{g},\green{a}) & (\blue{g},\green{b}) & (\blue{g},\green{c}) \end{matrix}\ \right] \end{array}\]

The depiction above is meant to provide an illustration of what actually occurs when multiplying two sets. The statement below is the proper notation.

\[\{e,f,g\}\times\{a,b,c\} = \{(e,a),(e,b),(e,c),(f,a),(f,b),(f,c),(g,a),(g,b),(g,c)\}\]

The final operation is flatten or flat map, represented by the $\bigcup$ symbol, and it works on sets of sets. It takes all the sets and flattens them into a single flat set containing the distinct items from all the sets. See the example below.

\[\bigcup \{ \{a,b,c\}, \{c,d,e\} \} = \{a,b,c,d,e\}\]

Notice how, just like the union operation, the result is the distinct items from all the sets. Thus concludes the demonstration of the five set operations.

Summary

Quick Review

A quick review of a few mathematical properties.

• Commutative property: Changing the order of the operands does not change the result: Assuming $\sigma$ is some arbitrary operation, $\sigma$ is commutative if $3 \sigma 4 = 4 \sigma 3$
• Associative property: The order in which the operations are preformed does not matter. Assuming $\sigma$ is some arbitrary operation, $\sigma$ is associative if $(2 \sigma 3) \sigma 4 = 2 \sigma (3 \sigma 4)$

Symbol	Name	Example	Properties	Identity
$\cup$	Union	\(\{1,2\} \cup \{2,3\} = \{1,2,3\}\)	Commutative, Associative	$A \cup \emptyset = A$
$\cap$	Intersection	\(\{1,2\} \cap \{2,3\} = \{2\}\)	Commutative, Associative	$A \cap \emptyset = \emptyset$, $A \cap \U = A$
$-$	Difference	\(\{1,2,4\} — \{2,3\} = \{1,4\}\)		$A - \emptyset = \emptyset - A = \emptyset$
$\times$	Cartesian Product	\(\{1,2\} \times \{2,3\} = \{(1,2),(1,3),(2,2),(2,3)\}\)		$A \times \emptyset = \emptyset \times A = \emptyset$
$\bigcup$	Flatten	\(\bigcup \{ \{1,2\}, \{2,3\} \} = \{1,2,3\}\)	N/A	$\bigcup{\emptyset} = \emptyset$

Exercises

1. Specify if each statement is true of false.
   a. $-1 \in \N$
   b. $\forall x \in \N, x \gt 0$
   c. $\exists \sigma \in \Z, \sigma \bmod 2 = 0$
   d. \(a \notin \{a,b,c\}\)
   e. \(\{0,1,2,\ldots\} = \Q\)
   f. \(\U - A = A^\prime\)

   Answers (click to expand)

   1. false - Negative numbers are not part of the $\N$ set.
   2. false - zero is included in $\N$ and it is not greater than itself.
   3. true - there is at least even number is the $\Z$ set
   4. false - $a$ is in the set
   5. false - $\Q$ has far more numbers than all the positive whole number including zero.
   6. true - the complement of set $A$ is all the items in $\U$ that are not in $A$

2. Assuming \(A = \{1,2,3,a\}\) and \(B = \{1,a,b,c\}\), calculate each set operation below:
   a. $A \cup B$
   b. $A \cap B$
   c. $A - B$
   d. $B - A$
   e. $A \times B$

   Answers (click to expand)

   1. $\{1,2,3,a,b,c\}$
   2. $\{1,a\}$.
   3. $\{2,3\}$.
   4. $\{b,c\}$.
   5. $\{(1,1),(1,a),(1,b),(1,c),(2,1),(2,a),(2,b),(2,c),(3,1),(3,a),(3,b),(3,c),(a,1),(a,a),(a,b),(a,c)\}$.

3. With regard to Cartesian products, answer the following questions.

   1. Regarding $A \times B = \{(a,b) \vert a \in A \; \text{and} \; b \in B\}$. Is $(a,b)$ equivalent to $(b,a)$?
   2. Is $A \times B$ equivalent to $B \times A$.
   Answers (click to expand)

   1. No, $(a,b)$ is NOT equivalent to $(b,a)$. Recall that the output of a multiplication operation is ordered pairs meaning that the order has meaning. Changing the order of the pair changes it's identity.
   2. No, unlike numbers, multiplication of sets is not commutative.
      $A = \{1,2\} \\ B = \{3,4\} \\ A \times B = \{(1,3),(1,4),(2,3),(2,4)\} \\ B \times A = \{(3,1),(3,2),(4,1),(4,2)\} $