Under Construction: Consider this content a preview of the real thing which is coming soon (hopefully).
The formal definition of the vertex cover problem is: given an undirected graph $G = (V,E)$, find the subset $V^\prime \subseteq V$ such that if $(u,v) \in E$, then $u \in V^\prime$ or $v \in V^\prime$ (or both). In plain English: find the smallest set of vertices in an undirected graph that include at least one end of each edge in the graph. The size of a vertex cover is the number of included vertices. Consider the example below:
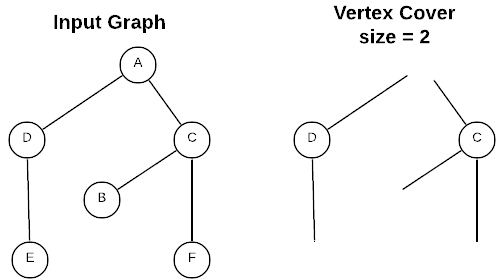
The vertex cover is the set \(\{D, C\}\) because that is the smallest set of vertices that includes at least one end of every edge in the graph.
Unfortunately, the vertex cover problem is $NP$-hard so it’s not possible to create an efficient algorithm capable of solving the general case. However, there are several reasonable approaches to the problem including:
- Solve for the special case
- Small vertex cover - When the vertex cover is small ($\approx \leq \log n$) the runtime is tractable. $O(2^k m)$ where $k$ is the size of the vertex cover
- Tree Graphs - Using a dynamic programming algorithm.
- Bipartite Graphs - Using an application of the maximum flow problem.
- If approximate answers will suffice, use a heuristics algorithm.
- Algorithm guaranteed to be no larger than twice the size of the optimal vertex cover
- If exact answers are a requirement, design an algorithm that’s exponential yet better than brute-force
Applications
- Fuzz testing algorithms
- Personnel scheduling (find the smallest set of people whom have a particular set of skills)
- Placing enough guards to cover an area
- Wireless telecommunication
- Circuit design
Asymptotic Complexity
Under Construction
Pseudo Code
Under Construction
Source Code
Relevant Files:
Under Construction
Click here for build and run instructions