This project contains many graph algorithms. This section provides a brief overview of graph concepts. Consider comprehension of this material a pre-requisite for graph algorithms.
Graphs represent pair wise relationships among objects. In graph jargon, the objects are known as either vertices or nodes. The relationship between the vertices are edges. Vertices that are connected via an edge are said to be adjacent to each other. To make the concept a bit more concrete, consider modeling one’s family as a graph. The people in the family would be vertices, and the relationships between them (mother, daughter, father, brother, etc..) would be edges. Edges are typically denoted by a pair known as the endpoints. If Dick is Jane’s brother, the relationship is denoted as $(Dick, Jane)$. The set of all vertices is denoted as $V$ and $E$ denotes the set of all edges. The degree of a vertex is the number of edges connected to it.
Graph Size
In order to accurately predict the performance of graph algorithms, it’s important to have common terminology for expressing the size of a graph. The size is made up of two components: the number of vertices and the number of edges. By convention, $n$ denotes the number of vertices and $m$ denotes the number of edges.
\[n = |V|\] \[m = |E|\]Graph density is important when determining the best way to represent a graph in memory. Consider a graph with no parallel edges, the lower bound of \(m\) is $n-1$. The upper bound of \(m\) is $\frac{n(n-1)}{2}$. Tree graphs conform to the lower bound and complete graphs have the maximum number of edges.
Roughly defined, a sparse graph is closer to the lower bound and a dense graph is closer to the upper bound.
Directed vs. Undirected Graphs
There are two types of graphs: undirected and directed. The edges of an undirected graph indicates a bi-directional relationship. $(A, B)$ and $(B, A)$ are essentially the same. See the example below.
Undirected Graph
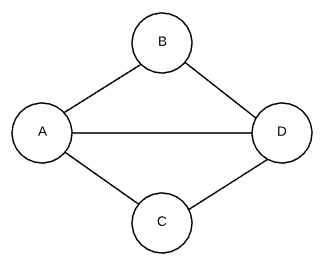
- $V: A, B, C, D$
- $E: (A, B), (A, C), (A, D), (B, D), (C, D)$
Conversely, the edges of a directed graph denote the direction of the relationship. $(A, C)$ indicates that A has a connection to C, but that does not imply that the reverse is also true. Continuing on with the family graph example, the brother edge $(Dick, Jane)$ indicates that Dick is Jane’s brother. However, Jane is not Dick’s brother. The end point of the relationship is known as the head while the origin is referred to as the tail. Some sources also refer to directed edges as arcs. See the example below.
Directed Graph
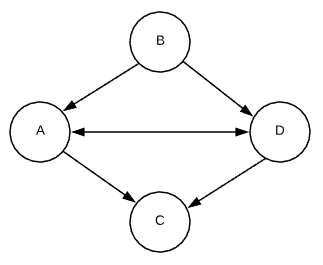
- $V: A, B, C, D$
- $E: (A, C), (A, D), (B, A), (B, D), (D, A), (D, C)$
Special cases of graphs
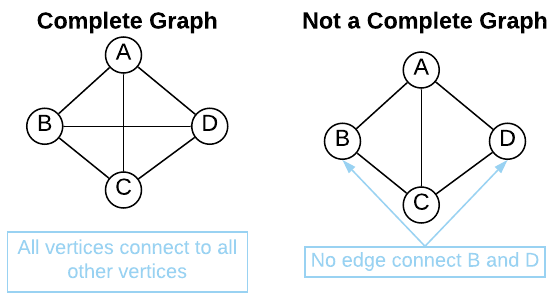
Complete Graph
Each pair of vertices in a complete graph is connected by an edge. Stated differently, it is an undirected graph in which every pair of distinct vertices is connected by a pair of unique edges. See the image below.
Tree
A tree is an undirected graph in which any two vertices are connected by exactly one edge. Stated differently, a tree is a connected acyclic undirected graph. See the example below.

Bipartite Graph
A bipartite graph (aka bi-graph) is a graph in which the vertices can be divided into two sets such that each edge connects a vertex in one set to a vertex in the other set. More formally, a graph $G = (V, E)$ is bipartite if it’s vertex set can be partitioned into two disjoint subsets $V = V_1 \cup V_2$, such that every edge has the form $e=(a,b)$ were $a \in V_1$ and $b \in V_2$. See the illustration below.
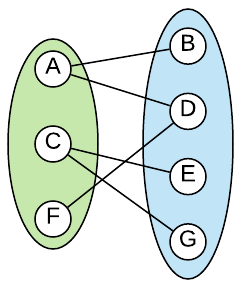
An alternate definition is a graph which there exists a cut so that every single edge is crossing it.
Cycle
An important concept related to directed graphs is cycles. A cycle occurs when there exists a vertex that has a path that leads back to itself. An example is shown below.
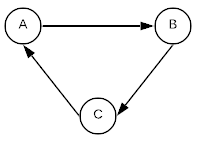
A graph that does not contain any cycles is said to be acyclic. The term Directed Acyclic Graph is often abbreviated to DAG.
Parallel Edges
A term commonly used in graph applications is parallel edge. A parallel edge is two or more edges related to the same two vertices. For instance, $(A, B)$ and $(B, A)$ are parallel edges. The edges in the graphic below are parallel edges.
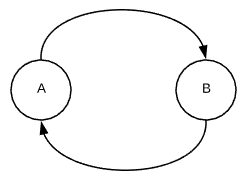
Edge Weights
Edges can also have weights associated with them. Weighting assigns a cost to each edge. Weighting can be modeled in almost any way imaginable. In a network, this weight could be connection latency. Going back to the family graph example. Each relationship edge could have an intimacy weight. For instance, a spousal relationship may have a weight of 5 whereas a sibling relationship may have a weight of 3. See the image below. In this graph, the $(Janice, Richard)$ edge has a higher weight than the $(Jane, Dick)$ edge.
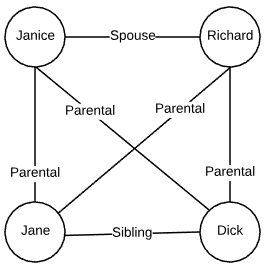
Connected Components (Undirected)
Portions of a Graph are said to be connected when there is no way to separate the vertices without edges crossing between the parts. A common task is to identify all connected components of a graph. Consider the graph below, it is made up of three connected components.
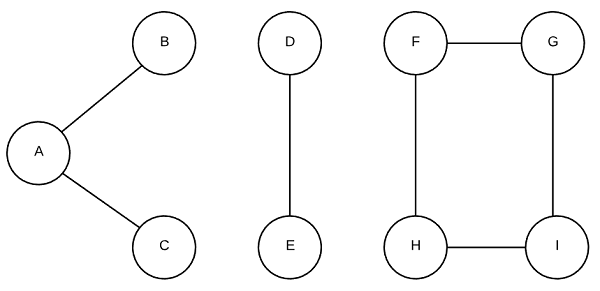
Strongly Connected Components (Directed)
Deciphering connected components in a directed graph is a bit more difficult than it is in undirected graphs. A strongly connected component is a subsection of a directed graph in which there is a directed path from every vertex to every other vertex. The rather convoluted graph below demonstrates the concept.
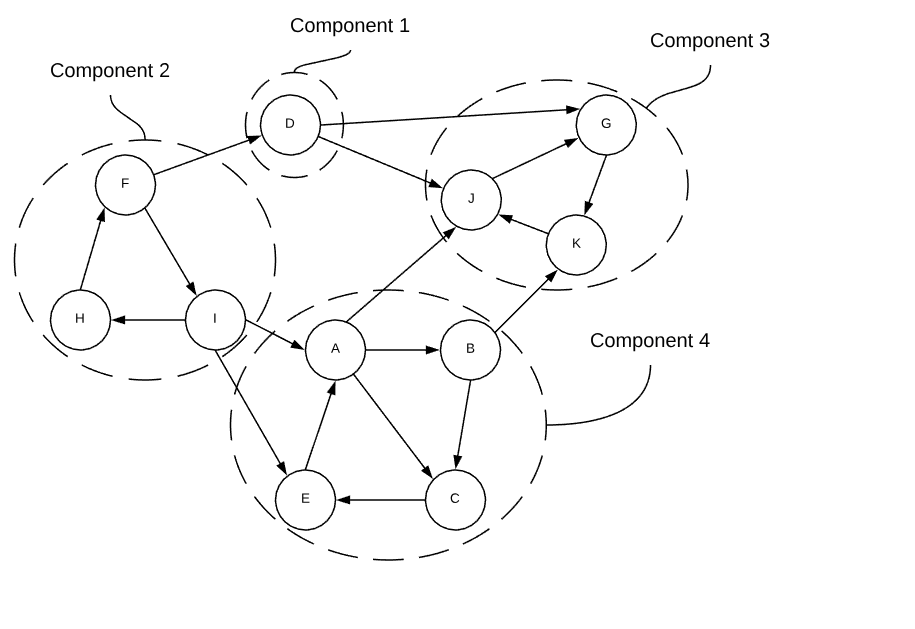
If each strongly connected component is treated as a single node, the graph becomes a directed acyclic graph. Just like nodes in a directed graph, a strongly connected components with no incoming edges is known as a source and one without any outgoing edges is known as a sink.
Minimum Cut
The minimum cut is the grouping of vertices into two non-empty groups having the fewest number of crossing edges. Consider the graph in the graphic below. There is no other way of dividing the vertices that would result in fewer crossing edges.
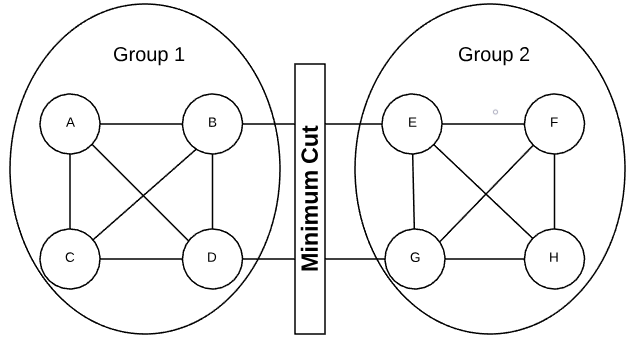
In an undirected graph, a crossing edge is considered any edge that has an end point in both groups. A crossing edge in a directed graph is when an edge has a tail in group 1 and a head in group 2. The minimum cut size is the number of crossing edges. Logically, the size cannot exceed the minimum degree of the graph.
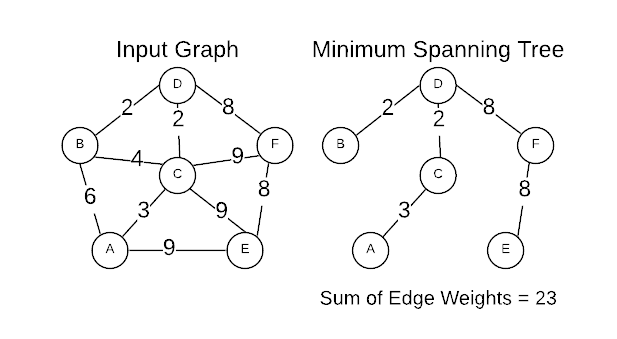
Minimum Spanning Tree
A Minimum Spanning Tree (MST) is the cheapest set of edges that connect graph vertices together. For instance, servers on a network or destinations on a road map. Stated differently, an MST is the sub-set of edges with the minimum possible sum of edge weights. A MST must satisfy two properties.
- Does not contain a cycle
- A path exists between every pair of vertices
Based on the definition of a MST, the following facts logically apply:
- All connected graphs have at least one MST
- There are often multiple valid MSTs for a given graph
- An MST has $n-1$ edges.
The image below is a graphical representation of an input graph and its MST.
Independent Set
Conceptually, an Independent Set (IS) is comparable to the inverse of a graph. It’s a set of vertices that do not contain both endpoints of any edge. Consider a connected graph with only three vertices as shown below. There are five independent sets.
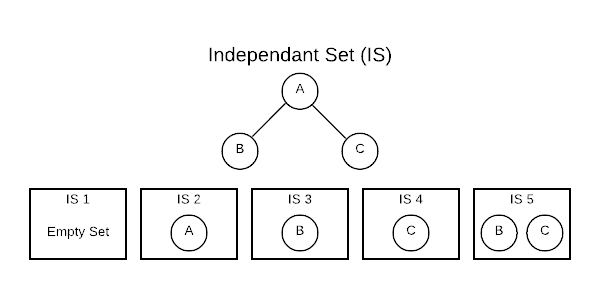
The [] (empty set) is always considered an IS because it technically fits the
definition. The sets [A], [B], and [C] are also ISs because no edge
contains only one vertex. The set [B, C] also qualifies because there are no
edges connecting B and C. One important thing to note is that the number of
ISs grows exponentially as the number of vertices grow. This has important
algorithmic implications.
At first glance, this concept seems a bit academic; however, ISs are useful in practice. Finding an IS is a way of asking, which vertices do not have a relationship. For instance, if vertices are people and edges are familial relationship, an IS would define people who are not related.
Path Graph
A path graph has vertices that can be listed in order $v_1, v_2, …,v_n$ such that edges are ${v_i, v_{i+i}}$ where $i = 1, 2, …, n-1$. That is rather complicated definition for a simple concept that is easily visualized. The image below represents a path graph.

There is only one path through the graph and each vertex is connected to the preceding vertex. By this definition, there will always be $n-1$ edges.
Topological Ordering (Acyclic Directed)
A graph with no cycles is said to be acyclic. A directed acyclic graph is particularly interesting because such graphs have a least one (usually many) topological ordering. A graph with a cycle has no topological ordering. While the goal of this project is to abstain from recondite mathematical definitions, this concept is much easier to understand in such terms. A topological sort is an ordering of vertices $v_{1},v_{2},…v_{n}$ in such a way, that if there exists an edge with a tail of $v_{j}$ and a head of $v_{i}$, then $v_{j}$ comes before $v_{i}$. It’s a ordering of vertices in which the directed edges of the graph always move forward in the ordering. Consider a graph in which the vertices represent tasks and directed edges represent precedence constraints. The topological orderings are acceptable sequences in which to complete the tasks. This is depicted graphically below.
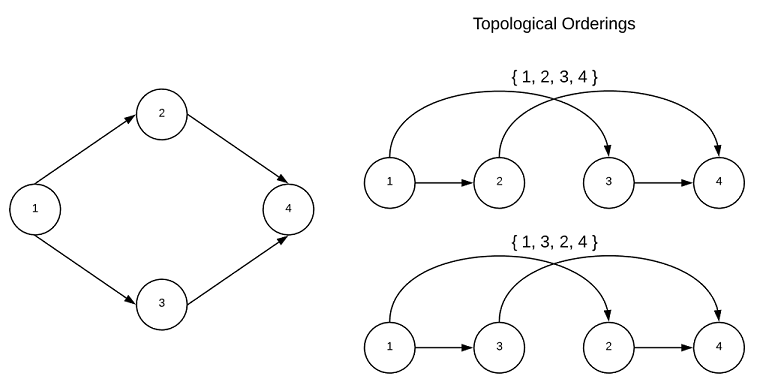
Every directed acyclic graph has a source vertex, that is a vertex with no incoming edges. Additionally, there must exists a vertex with no outgoing edges known as the sink vertex. The interested reader is encouraged to contemplate why this is true…
Graph Representations
There are several ways of representing a graph. Two of the most common are adjacency matrices and adjacency lists. The choice of which to use depends on graph density (sparse vs dense) as well as the desired graph operations.
For both cases, consider the graph below.

Adjacency Matrix
An adjacency matrix depicts vertices as indices across the top and side of a matrix. A one at the intersection of two vertices indicates a connected edge while a zero indicates no connection. The associated adjacency matrix for the graph in question is shown below.
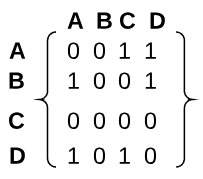
The amount of space required to store an adjacency matrix is $n^2$.
Adjacency List
There are several different ways to create an adjacency list. However, the general concept is to have four components:
- Array of Vertices
- Array of Edges
- Edges have two pointers, one for the tail and one for the head
- Vertices have one pointer for each of its edges
One common adjacency list representation is an array of linked lists. Each item in the array is a vertex. Each edge is represented as a link.
Vertices
[
{ A -> C -> D -> NULL }
{ B -> A -> D -> NULL }
{ C -> NULL }
{ D -> C -> A -> NULL }
]
Depending on the application’s needs, keeping the vertices and edges in separate arrays may be more appropriate as show below.
Vertices Edges
[ [
{ A, [0, 1] } [0]{ A, C }
{ B, [2, 3] } [1]{ A, D }
{ C, NULL } [2]{ B, A }
{ D, [4, 5] } [3]{ B, D }
] [4]{ D, C }
[5]{ D, A }
]
Adjacency lists have lower space requirements than matrices. Additionally, they are optimized for graph search algorithms.
Applications
There are virtually countless applications for graphs. Below are just a few common uses.
- Road Networks (driving directions) - roads are vertices are intersections are edges
- Networks - machines are vertices and connections are edges
- Social Networks - people are vertices and relationships are edges
- Web - pages are the vertices and hyperlinks are the edges
- Genealogy - people are the vertices and family relationships are the edges
- Academic Plans: Courses are vertices and prerequisites are directed edges
Source Code
Relevant Files:
All of the graph algorithms utilize this graph code which is located in the
utils/cdirectory. This is a general purpose graph with an Adjacency List representation.
Click here for build and run instructions