Insertion Sort

graph LR
	ALG(["fas:fa-trophy Insertion Filter fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	ARRAY(["fas:fa-check Array #160;"])
    click ARRAY "./list-data-struct-array"

	LL(["fas:fa-check Linked List #160;"])
    click LL "./list-data-struct-linked-list"

	ASY_ANA-->ALG
	ARRAY-->ALG
	LL-->ALG

Insertion sort is another simple sorting algorithm. Like bubble sort, it’s has a quadratic ($O(n^2)$) runtime; however, recall from the Real World Asymptotic Complexity section that asymptotic complexity is a single data point and not a holistic measure of efficiency. There are many factors that contribute to execution time as measured by a clock. In practice, insertion sort is as much as three times faster than bubble sort¹.

History

The origin of insertion sort is difficult to ascertain as it pre-dates computing. However, it’s first use in a computation context traces back to 1945 when Konrad Zuse defined it as a primitive for the first high-level programming language: Plankalkül. The word Plankalkül is roughly translated to “program calculus”. Although Zuse meticulously defined the language, it was never actually implemented. It’s unfortunate that world was never able to actually use the first high-level programming language.

The animated image below illustrates the insertion sort algorithm. Examine the pseudo code in conjunction with the graphic to understand how it works.

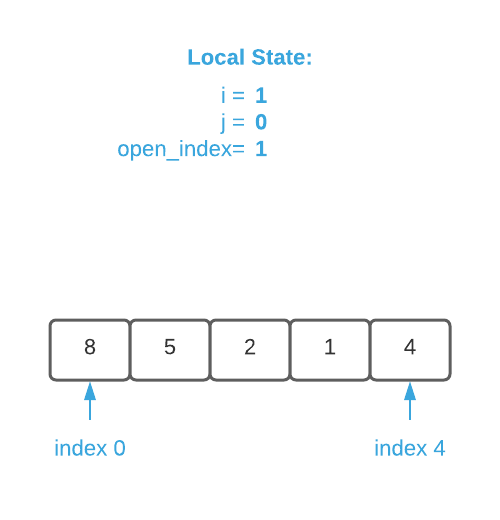
Notice how the algorithm commences at the beginning of the data and works it’s way to the end. This is notable because there are some situations where all the data isn’t immediately available and insertion sort allows you to sort as the data arrives. There are other algorithms with more desirable asymptotic complexities; however, this feature makes insertion sort uniquely suited for some scenarios.

Pseudo Code

\begin{algorithm}
\caption{Insertion Sort}
\begin{algorithmic}
\REQUIRE $A$ = list of numbers
\ENSURE $A$ sorted in sequential order
\FUNCTION{insertionSort}{$A$}
    \FOR{i $\gets$ 1 to $\vert A \vert$ - 1}
        \STATE open-index $\gets$ i
        \STATE temp $\gets A_i$
        \STATE
        \FOR{j $\gets$ (i-1) to 0}
            \IF{temp $\lt A_j$}
                \STATE $A_{\text{open-index}} \gets A_j$
                \STATE open-index $\gets$ open-index - 1
            \ELSE
                \BREAK
            \ENDIF
        \ENDFOR
        \STATE
        \STATE $A_{\text{open-index}} \gets$ temp
    \ENDFOR
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Asymptotic Complexity

$O(n^2)$

Source Code

Full Repo

Relevant Files:

• insertion_sort.h
• insertion_sort.c
• insertion_sort_test.c

Click here for build and run instructions

Exercises

1. Using the insertion sort pseudo code as a guide, what incoming data configuration will result in:
   a. the worst possible runtime
   b. the best possible runtime

   Answers (click to expand)

   1. If the data is in reverse order, the result is the upper bound as defined by the asymptotic complexity analysis ($O(n^2)$). The inner loop will always iterate through every item in the current sub-section of the array.
   2. If the data is pre-sorted, the runtime will be linear ($O(n)$). The inner loop will always terminate on line 11 during its first iteration.

2. Using the programming language of your choice, implement an insertion sort function that accepts:
   • an array of any type
   • a sorting strategy
   Answers (click to expand)

   See the C implementation provided in the links below. Your implementation may vary significantly and still be correct.
   - insertion_sort.h
   - insertion_sort.c
   - insertion_sort_test.c

3. The super_sport.txt file contains a list of names and scores for the fictional game super sport in the following format.

   <FIRST NAME><space><LAST NAME><tab><SCORE>

   In super sport, contestants earn a score between 1 and 10 with lower scores being the most desirable. Your task is to write a score tracking function that accepts a single contestant result (name-score tuple) and tracks a running list of results in wining order. The function must have a linear $(O(n))$ runtime (per invocation). Write a separate function that parses the file and pushes the results to the scoring function one at a time. The overall algorithm must have a quadratic ($O(n^2)$) runtime. Finally, print out the top 10 winning scores. The final interface should be similar to:

   void score_tracker(score_list, contestant_result) {
    // add contestant_result to score_list in sorted order
   }
   
   void parse_file(file_path) {
    // call score_tracker for each line in the file
   }
   
   void print_top_ten(score_list) {
    // print top 10 contestant names and scores
   }
   

   HINT: You will need a slightly modified version of an insertion sort algorithm. The linear runtime requirement precludes storing the running results in an array.

   Answers (click to expand)

   See the C implementation provided in insertion_sort_test.c Your implementation may vary significantly and still be correct. For reference, the printed output should be:
   1 Brandon Powell 0.163006
   2 Audrey Coleman 0.200230
   3 Cameron Kelly 0.392803
   4 Gabrielle Kelly 0.630958
   5 Trevor Gill 0.641713
   6 Isaac Manning 0.697553
   7 Penelope Greene 0.860558
   8 Colin Parr 1.088088
   9 Carl Newman 1.297904
   10 Deirdre Springer 1.37231