Binary Tree

graph LR
	ALG(["fas:fa-trophy Binary Tree fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	ARRAY(["fas:fa-check Sorted Array #160;"])
    click ARRAY "./list-data-struct-sorted-array"

	LL(["fas:fa-check Linked List #160;"])
    click LL "./list-data-struct-linked-list"

	ASY_ANA-->ALG
    ARRAY-->ALG
    LL-->ALG

Just like arrays and linked lists, binary trees are a popular list data structure¹. As the name implies, binary trees arrange data in a tree like² structure with a root, branches, and leaves as illustrated below³. Each tree node has a left and a right pointer. Navigating nodes is a series of binary (left or right) decision.

History

The precise origin of binary trees is difficult to ascertain. Several papers from the late fifties and early sixties develop the concept.

• 1959 Techniques for the Recording of, and Reference to data in a Computer by Alexander S. Douglas
• 1962 Some Combinatorial Properties of Certain Trees With Application to Searching and Sorting by Thomas N. Hibbard
• 1960 Trees, Forests, and Rearranging by P. F. Windley
• 1960 On the Efficiency of a New Method of Dictionary Construction by Andrew D. Booth and Andrew J.T. Colin

As with many scientific advancements, it appears that multiple researchers simultaneously converged on the concept⁴.

The memory layout of a doubly linked list and a binary tree are identical: both list data structures have nodes that store arbitrary data and two pointers. The difference is that they maintain distinct invariants. In a doubly linked list, the pointers point to the previous and next nodes while binary tree pointers point to left and right nodes. Exactly what is meant by left and right is covered below but first it’s important to define invariant.

Invariant

Core to the study of algorithms are algorithmic invariants. Invariant is a term borrowed from mathematics. It is a property that remains unchanged regardless of the applied operation or transformation. For instance, the ratio of the circumference to the diameter of a circle ($\pi$) is an invariant. No matter what you do to a circle this property remains unchanged. Any operation that invalidates the invariant results in something other than a circle.

Almost all algorithms have invariants. For instance, a linked list must maintain next pointers pointing to the next ordinal item in the list. Any operation that invalidates this invariant results in something other than a linked list. The sort order of a sorted array is another example. For binary trees, the definition of left and right is an invariant. If a binary tree maintains the invariant that items to the left have lesser values and items to the right have greater values, it’s said to be a binary search tree.

Binary Search Tree

There are actually many different flavors of binary tree with the differentiating factor between them being their invariants. Binary search trees are the most common and least complex so they are the subject of this section. Two binary search tree invariants are:

• Every descendant to the left of a given node has a lesser value than its parent
• Every descendant to the right of a given node has a greater value than its parent

As an example, consider the binary search tree of integers depicted in the drawing below. The arrangement of data makes the binary search⁵ algorithm inherent to the data structure. Starting at the root node, simply follow the left or right pointers until you reach the desired value.

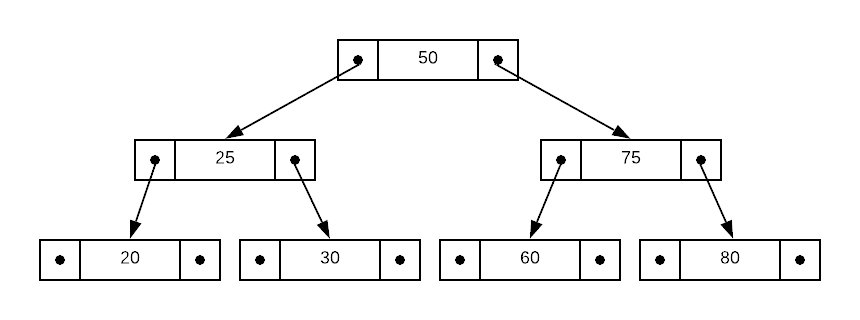
An interesting property of binary search trees is that there are multiple valid ways to maintain the invariants. For instance, consider the tree depicted below; it has the same data as the image above. Both configurations honor the invariants and are therefore valid. This phenomenon makes insertions easy as it is always possible to insert a new node without rearranging existing nodes.

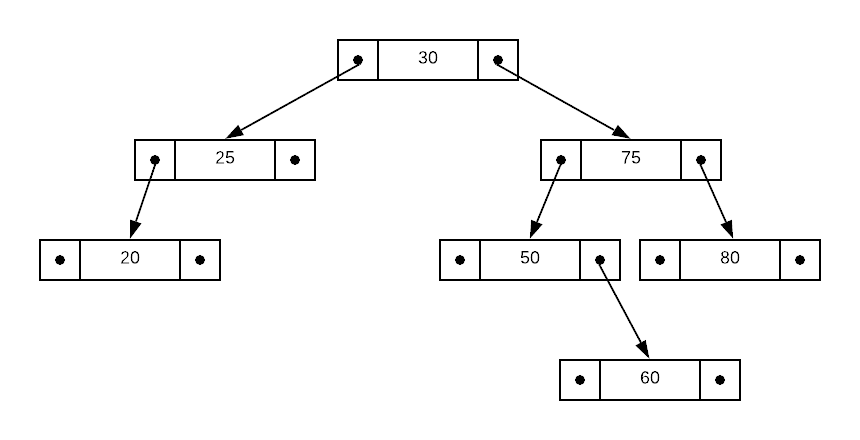
Because binary search trees have efficient insert and search operations, they are an excellent option when you need to repeatedly search an evolving list of data. What is shown thus far is the simplest possible implementation. A few enhancements to the model provide additional utility.

Adding Functionality

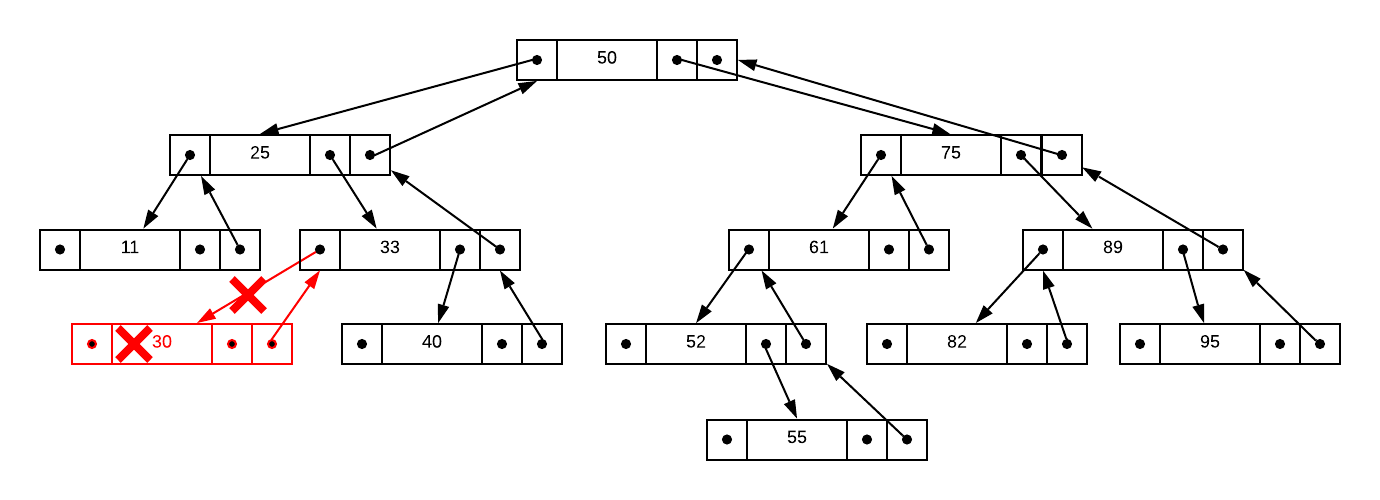
Binary search trees, as described thus far, support the insert, search, enumerate, min, and max operations (see the pseudo code section for details). However, supporting the delete, predecessor⁶, and successor⁷ operations require adding a parent pointer that points to the node directly above it. To make this a bit more concrete, consider the binary search tree depicted below.

Suppose we want to delete the integer 30. This case is easy because it resides in a leaf. In order to delete the node, we simply follow the parent pointer and set the resulting node’s left (or right in some situations) pointer to NULL. This is depicted graphically in the image below.

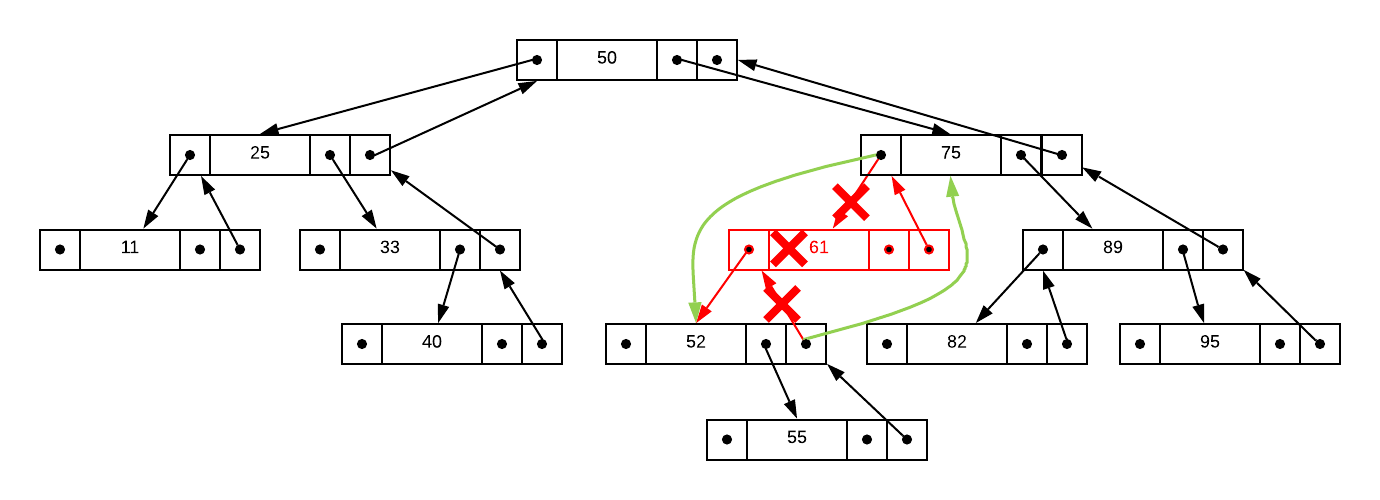
Now, assume you need to delete 61 from the tree. This is slightly more complex because it has a child. In this case, the parent pointer must be redirected to the child. The graphic below illustrates the concept.

Consider one last scenario that is even more complex. Suppose you need to delete a node that has two children, which we will denote as $\alpha$. The first step is to find the node with the largest value in $\alpha$’s left sub-tree⁸ which we will denote as $\beta$. Next, update $\alpha$’s value to $\beta$’s value⁹. Finally, delete $\beta$. Because $\beta$ holds a maximum value, it will be either a leaf or single child and will therefore conform to one of the scenarios presented in the previous paragraphs. Applying this to the tree illustrated above, assume you need to delete the integer 75 which has two children: 52 and 89. The first step is to find the largest value in 75s left sub-tree which is 55 in this case. Simply update the node in question to this value and delete the leaf. The graphical depiction is particularly helpful in this case.

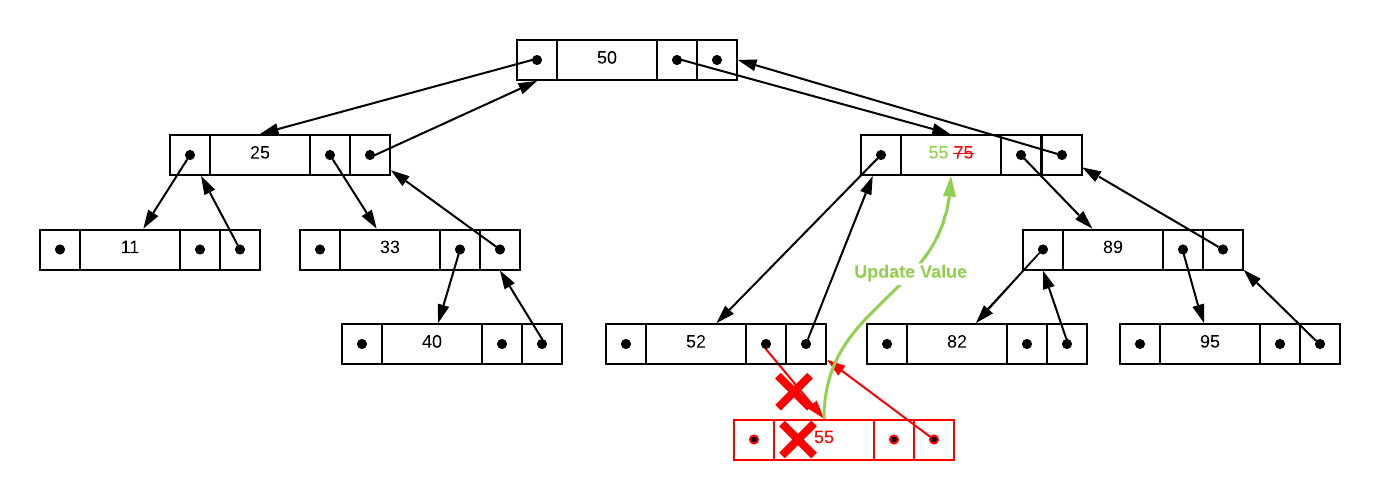
Hopefully, the breakdown of the delete operation elucidates the need for parent pointers. The reader is encouraged to study the predecessor and successor pseudo code and convince themself that parent pointers are also necessary for those operations.

Applications

• Countless general purpose programming tasks
• Primary data structure for Huffman Codes
• Database indexes
• Binary space partitioning algorithm used in video games
• Syntax trees used by compilers

Pseudo Code

\begin{algorithm}
\caption{Binary Search Tree Operations}
\begin{algorithmic}
\REQUIRE node = root node of a binary search tree
\REQUIRE item = item to insert
\FUNCTION{insert}{node, item}
  \IF{item $\lt$ node}
    \IF{node.left = NULL}
        \STATE{node.left $\gets$ item}
    \ELSE
        \STATE \CALL{insert}{node.left, item}
    \ENDIF
  \ELSE
    \IF{node.right = NULL}
        \STATE{node.right $\gets$ item}
    \ELSE
        \STATE \CALL{insert}{node.right, item}
    \ENDIF
  \ENDIF
\ENDFUNCTION
\STATE
\REQUIRE node = node to delete
\FUNCTION{delete}{node}
    \IF{node has 0 children}
        \STATE delete pointer to node in parent node
    \ELSEIF{node has 1 child}
        \STATE update node parent to point to child
    \ELSEIF{node has 2 children}
        \STATE largest-left $\gets$ \CALL{max}{node.left} 
        \STATE node.value $\gets$ largest-left.value
        \STATE \CALL{delete}{largest-left}
    \ENDIF
\ENDFUNCTION
\STATE
\REQUIRE node = binary search tree root node
\REQUIRE val = value to search for
\OUTPUT node if value is found, otherwise $\text{NOT_FOUND}$
\FUNCTION{search}{node, val}
    \IF{node = NULL}
        \RETURN $\text{NOT_FOUND}$
    \ELSEIF{node.value = value}
        \RETURN node
    \ELSEIF{node.value $\lt$ value}
        \RETURN \CALL{search}{node.left, value}
    \ELSE
        \RETURN \CALL{search}{node.right, value}
    \ENDIF
\ENDFUNCTION
\STATE
\REQUIRE node = binary search tree root node
\REQUIRE func = function to apply to each item
\FUNCTION{enumerate}{node, func}
    \IF{node = NULL}
        \RETURN
    \ENDIF
    \STATE \CALL{enumerate}{node.left}
    \STATE \CALL{func}{node}
    \STATE \CALL{enumerate}{node.right}
\ENDFUNCTION
\STATE
\REQUIRE node = binary search tree root node
\OUTPUT node containing minimum value in the tree
\FUNCTION{min}{node}
    \IF{node.left = NULL}
        \RETURN{node}
    \ELSE
        \RETURN \CALL{min}{node.left}
    \ENDIF
\ENDFUNCTION
\STATE
\REQUIRE node = binary search tree root node
\OUTPUT node containing maximum value in the tree
\FUNCTION{max}{node}
    \IF{node.right = NULL}
        \RETURN{node}
    \ELSE
        \RETURN \CALL{max}{node.right}
    \ENDIF
\ENDFUNCTION
\STATE
\REQUIRE node = any binary tree node
\OUTPUT node ordered directly before node
\FUNCTION{predecessor}{node}
    \IF{node.left $\neq$ NULL}
        \RETURN \CALL{max}{node.left}
    \ENDIF
    \RETURN first parent node where value $\lt$ node.value
\ENDFUNCTION
\STATE
\REQUIRE node = any binary tree node
\OUTPUT node ordered directly after node
\FUNCTION{successor}{node}
    \IF{node.right $\neq$ NULL}
        \RETURN \CALL{min}{node.right}
    \ENDIF
    \RETURN first parent node where value $\gt$ node.value
\ENDFUNCTION
\STATE
\REQUIRE root = binary search tree root node
\REQUIRE node = binary tree node to find rank for
\REQUIRE offset = accumlative offset of the index (default to zero)
\FUNCTION{rank}{root, node, offset}
    \STATE left $\gets$ number of items in left subtree
    \IF{root = node}
        \RETURN left + offset
    \ELSEIF{root.value $\lt$ node.value}
        \RETURN \CALL{rank}{root.left, node, offset}
    \ELSE
        \RETURN \CALL{rank}{root.right, node, offset + left + 1}
    \ENDIF
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Implementation Details

Each operation in the pseudo code accepts or returns a binary tree node. Assuming that you are trying to create a general purpose binary search tree, this is a bad practice. Giving outside callers direct access to the nodes provides them the opportunity to destroy your invariants as demonstrated in the code snippet below.

// Search for any random value
node result = search(&root_node, 10);
// Look at me, I'm soiling the sanctity of the invariant
result.left = &root_node;

A better approach is to provide an abstraction that allows consumers to work directly with node values. This is how binary search trees are implemented in the supplied source code.

Asymptotic Complexity

• Insert: $O(\log_{2}n)$
• Delete: $O(\log_{2}n)$
• Search: $O(\log_{2}n)$
• Enumerate: $\Theta(n + \log_{2}n)$
• Min: $O(\log_{2}n)$
• Max: $O(\log_{2}n)$
• Predecessor: $O(\log_{2}n)$
• Successor: $O(\log_{2}n)$
• Rank: $O(\log_{2}n)$

Advantages

• Search: Optimized for quick search operations
• Insert/Delete: Although slower then linked list, considerably faster than arrays.
• Maintains Sort Order: Maintains sorted order regardless of insertion order.

Disadvantages

• Memory: Each node must maintain two or more additional pointers.
• Spatial Locality: It’s possible to distribute items throughout memory in a non-optimal way.
• Maintains Insertion Order: The order in which items are inserted is lost.
• Complexity: The most complex list data structure.

Source Code

Full Repo

Relevant Files:

• binary_tree.h
• binary_tree.c
• binary_tree_test.c

Click here for build and run instructions

Exercises

1. Assuming a 64-bit architecture, what is the total amount of memory required to store 128 64-bit integers in a binary search tree that supports the following operations:
   a. Insert and search
   b. Insert, search, and delete
   c. Insert, search, delete, successor, and predecessor

   Answers (click to expand)

   1. Each of the 128 nodes requires a 64-bit integer, a 64-bit left pointer, and a 64-bit right pointer amounting to 24 bytes. The total amount of memory is therefore $24 \text{bytes} * 128 \text{nodes} = 3072 \text{bytes}$.
   2. Recall that the delete operation require an extra parent pointer. Therefore, each of the 128 nodes requires a 64-bit integer, a 64-bit left pointer, a 64-bit right pointer, and a 64-bit parent pointer amounting to 32 bytes. The total amount of memory is $32 \text{bytes} * 128 \text{nodes} = 4096 \text{bytes}$.
   3. The answer is the same as b. There is no extra data required to support the successor and predecessor operations.

2. Which of the following are binary search tree invariants. Assume that insert and delete operations are a requirement.
   a. Every node other than root should have a pointer to it’s parent node
   b. The value of a parent node is always greater than it’s child nodes
   c. Every descendant to the left of a given node has a lesser value
   d. Every node must maintain an integer value

   Answers (click to expand)

   1. This is an invariant. Failing to maintain this property will break the delete operation.
   2. This is not an invariant. Every child to the right of a node has a higher value.
   3. This is an invariant. Failing to maintain this property will break the search operation.
   4. This is not an invariant. Nodes can maintain arbitrary data.

3. Identify the invariant violation in the binary search tree depicted below.

   

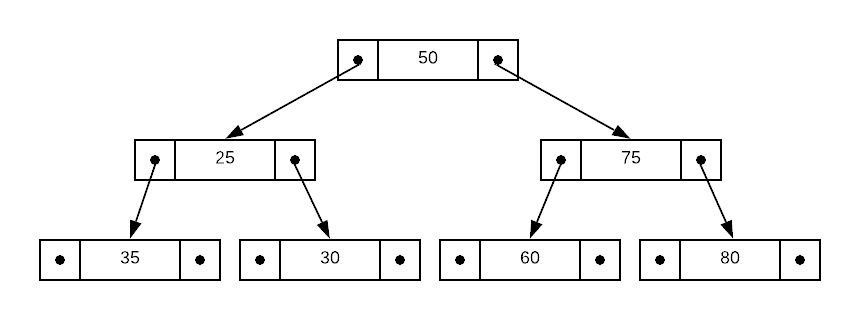
   Answers (click to expand)

   The "every descendant to the left of a given node has a lesser value" invariant is violated. 35 is not less than 25.

4. True or false: There is only one valid way to arrange data in a binary search tree that maintains the invariants.

   Answers (click to expand)

   False. There are several valid ways to arrange data in a binary search tree and still maintain the invariants. Review the binary search tree section for details.

5. Using the image below as a starting point, draw what the binary search tree will look like after deleting the 40 and 150 nodes.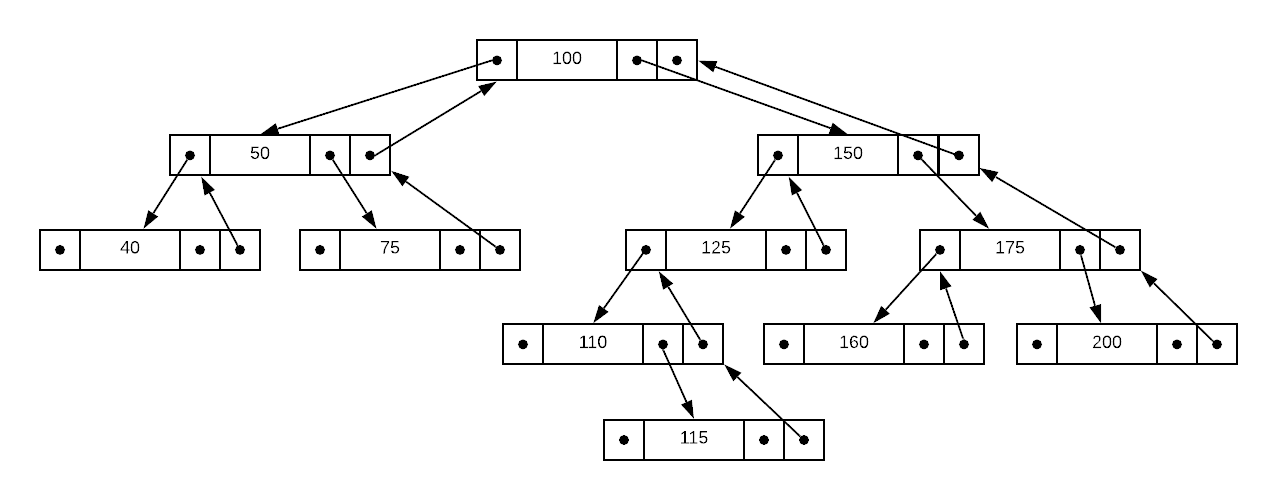

   

   Answers (click to expand)

   

6. Using the binary tree illustrated below and the supplied pseudo code, specify the number of parent pointers that must be followed to find the predecessor for:
   a. 125
   b. 160
   c. 115
   d. 100

   

   Answers (click to expand)

   1. 125's predecessor is 115. The answer to the question is 0. The condition on line 66 of the pseudo code evaluates to false, so finding the predecessor is matter of identifying the max value in the left sub-tree.
   2. 160's predecessor is 150. The answer to the question is 2. Line 70 of the pseudo code recursively follows parent pointers until it arrives at a value less than the target node's value. In this case, that is two pointers away.
   3. 115's predecessor is 110. The answer to the question is 1. Line 70 of the pseudo code will halt at the first parent because it's value is less than 115.
   4. 100's predecessor is 75. The answer to the question is 0. The condition on line 66 of the pseudo code evaluates to false, so finding the predecessor is matter of identifying the max value in the left sub-tree.

7. Carefully examine the BinaryTreeNode struct in the binary_tree.h file and notice the size property. Also notice that the InsertNode function in the binary_tree.c file increments size when adding a new node. Answer the two questions below.
   Hint: the operation is specified in the pseudo code but was not discussed in the writing.
   a. What operation does the size property support.
   b. Is it possible to support said operation without the size property.

   Answers (click to expand)

   1. The size property supports the rank operation. Notice line 81 of the pseudo code. It's necessary to calculate the number of items in the left sub-tree node. The cached size value makes this calculation easy.
   2. Technically, yes; it's possible to use the enumerate operation to visit every node in the left sub-tree and calculate the rank. However, this would needlessly increase rank's asymptotic complexity. Caching size during insert and delete operations is a better solution.