Prerequisites (click to view)
graph LR
ALG(["fas:fa-trophy Self Balancing Binary Tree fas:fa-trophy #160;"])
ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
click ASY_ANA "./math-asymptotic-analysis"
BT(["fas:fa-check Binary Tree #160;"])
click BT "./list-data-struct-binary-tree"
ASY_ANA-->ALG
BT-->ALG
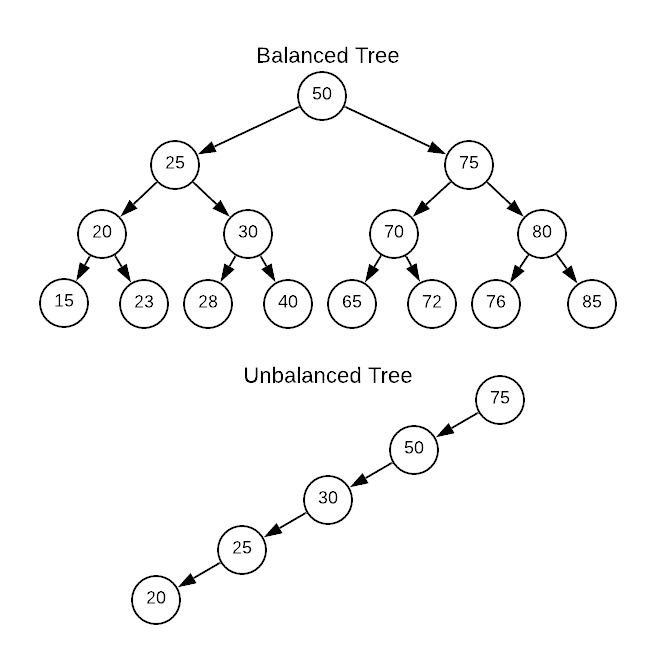
The previous section on Binary Trees took a few liberties concerning asymptotic complexity. The purpose was to meter the amount of new concepts introduced; however, with the introductory concepts out of the way it’s time to correct the oversight. While most operations were advertised as $O(\log_{2}n)$, in reality, this is only true if the tree is perfectly balanced. A balanced tree has an equal number of children to the left and right of each node1 as illustrated in the binary search tree of integers below. A more accurate measure of a tree’s asymptotic complexity is derived from the tree’s height.
History
After the invention of binary trees, it didn’t take long for self-balancing trees to evolve. Two Russian mathematicians, Georgy Adelson-Velsky and Evgenii Landis, published a paper entitled An Algorithm for the Organization of Information in 19622 which outlined a technique for maintaining balance. The resulting data structure was named AVL tree after the initials of the inventors’ last names. AVL trees are still commonly used today.
Tree Height
A more accurate measure of a tree’s asymptotic complexity is derived from the tree’s height. The height of a tree is the number of nodes from the root to the most distant leaf. See the image below for a graphical reference.
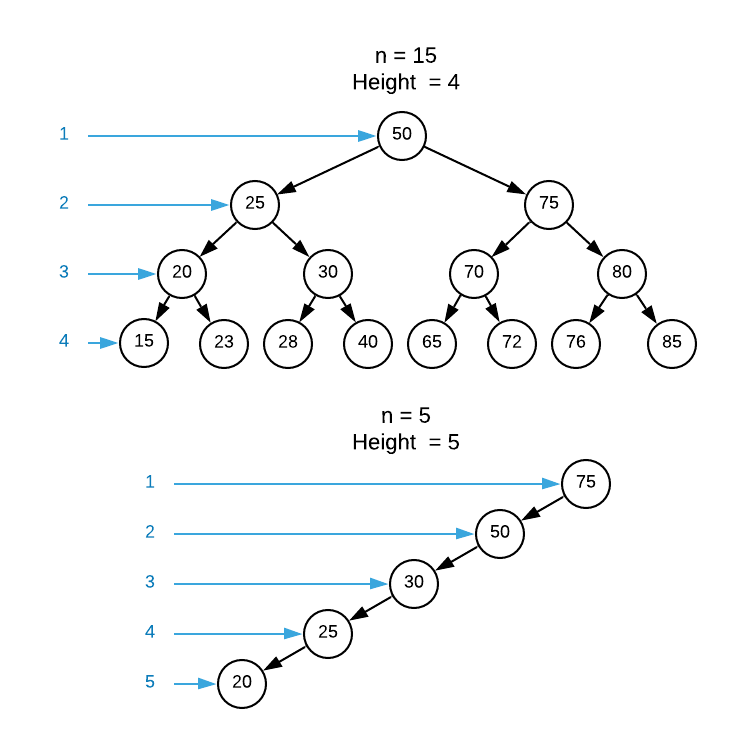
Using the previously defined search operation, calculate the worst case number of comparisons required to locate a node in both trees shown above. Take a few minutes to come up with an answer before reading on.
Even though the balanced tree has three times more items, there are fewer requite comparisons (4 for the balanced tree and 5 for the unbalanced tree). The disparity compounds with more nodes. Stated more rigorously, the search operation has a runtime of $O(\text{height})$. Although this seems in opposition to the assertion that search is an $O(\log_{2}n)$ operation for a balanced search tree, consider the maximum height. Notice how the bottom row of nodes has exactly twice as many items as the row above it. This patterns continues all the way to the root. A number repeatedly divided by 2 is $\log_2$. Therefore, the height of a balanced search tree is $\log_2{n}$.
Conversely, the height of an completely unbalanced tree is $n$. $O(\text{height})$ works out to logarithmic ($O(\log_{2}n)$) for a balanced tree and linear ($O(n)$) for an unbalanced tree. As a reminder of the significant difference between the two complexity classes, see the comparison table below.
| Input size $n$ | $O(n)$ linear | $O(log_2{n})$ logarithmic |
|---|---|---|
| 10 | 10 | 4 |
| 100 | 100 | 7 |
| 1000 | 1000 | 10 |
| 10000 | 10000 | 14 |
| 100000 | 100000 | 17 |
| 1000000 | 1000000 | 20 |
| 10000000 | 10000000 | 24 |
Perusal of the binary search tree pseudo code reveals that all the operations have a traversal mechanism similar to search. This means that all operations become linear for an unbalanced tree. As is hopefully clear by now, balance is a major concern with trees.
Maintaining Balance
Luckily, there are many well-defined tree data structures with built-in self-balance mechanisms. These are know as self balancing search trees. Examples of such trees include, but are not limited to:
- AVL trees
- Red-black trees
- Splay trees
- AA trees
- B-trees
- 2-3 trees
- 2-3-4 trees
- Scapegoat trees
- Treaps
- Weight-Balanced trees
- etc…
Many of the examples listed above are simply enhanced binary trees that cleverly rearrange nodes in order to maintain balance. However, some are more exotic, such as B-trees which accommodate many keys per node. Each variation has slightly different runtime characteristics and utility. It’s not practical to cover all variations owing to the breadth of the topic. One could write a book solely on tree data structures. In the event that the reader has a performance critical application for trees3 it’s highly recommended that they delve deeper into this topic.
This begs the question, if there are trees capable of self balancing, why would anyone use a standard Binary Tree? The answer is that there is overhead associated with maintaining balance in the form of both complexity and clock cycles4. Self balancing ensures optimal tree traversals at the cost of less than optimal delete and insert operations5. Therefore, the ratio of insert/delete to traversal operations is a consideration. In cases where data is inserted in random order, statistically, a standard binary tree will be balanced regardless6. As with most cases in computer science, the particular circumstances determine the optimal solution. There is no one right answer.
The next obvious question is how exactly do self balancing trees maintain balance? While each implementation is unique, rotations are a prominent technique.
Rotations
Conceptually, a rotation is a procedure for rewriting node pointers so that a parent node trades places with one of it’s children in order to to reduce the overall height of the tree. A left rotation swaps the parent with its right sibling while a right rotation swaps the parent with its left sibling. Rotations are difficult to put in writing but easy to represent graphically. Consider the simplest possible rotation scenario: a tree with only three nodes as depicted below.
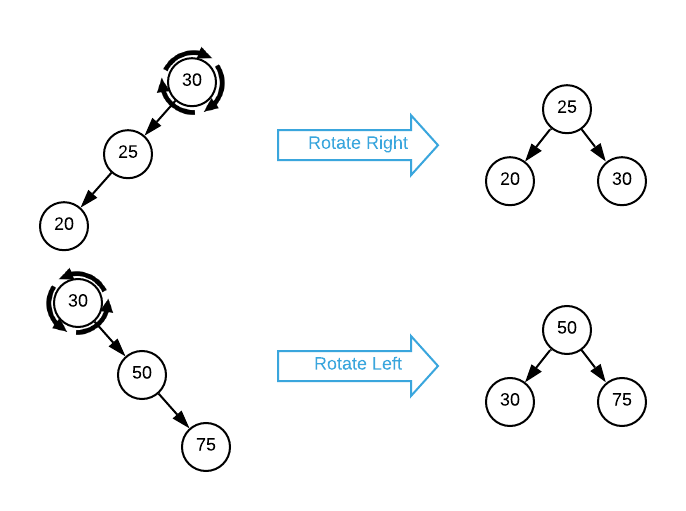
At a minimum, a rotation consists of rewriting two pointers. For instance, the left rotation shown above sets the rotate node’s right pointer to NULL and changes the right child’s left pointer to the address of the rotated node7. Of course, things get more complicated when there are child nodes to contend with. Consider a left rotation as illustrated below.
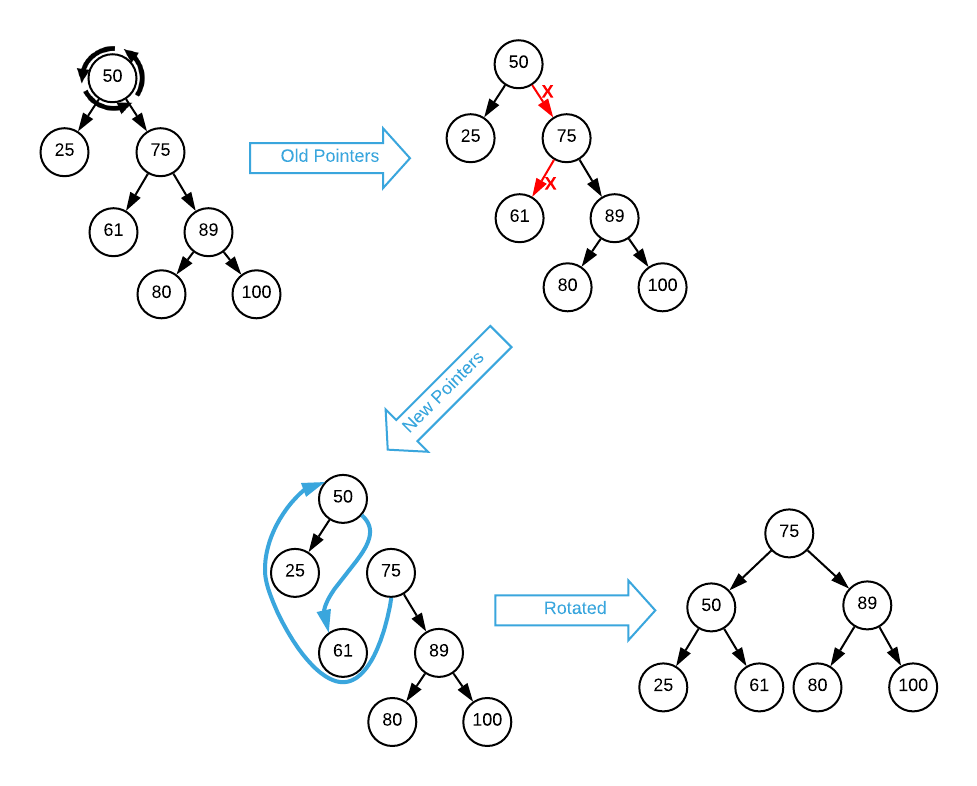
Take a minute to examine the image. In order to rotate the root node (50) to the left, three things must happen:
- The parent of the rotation node (50) becomes the parent of the right node (75). In this case, NULL.
- The rotation node’s (50) right pointer is updated to the right node’s left pointer
- The right node’s (75) left pointer changes to the rotation node (50)
A similar process occurs when rotating right. In this example, a branch node (75) is rotated. Consult the image below.
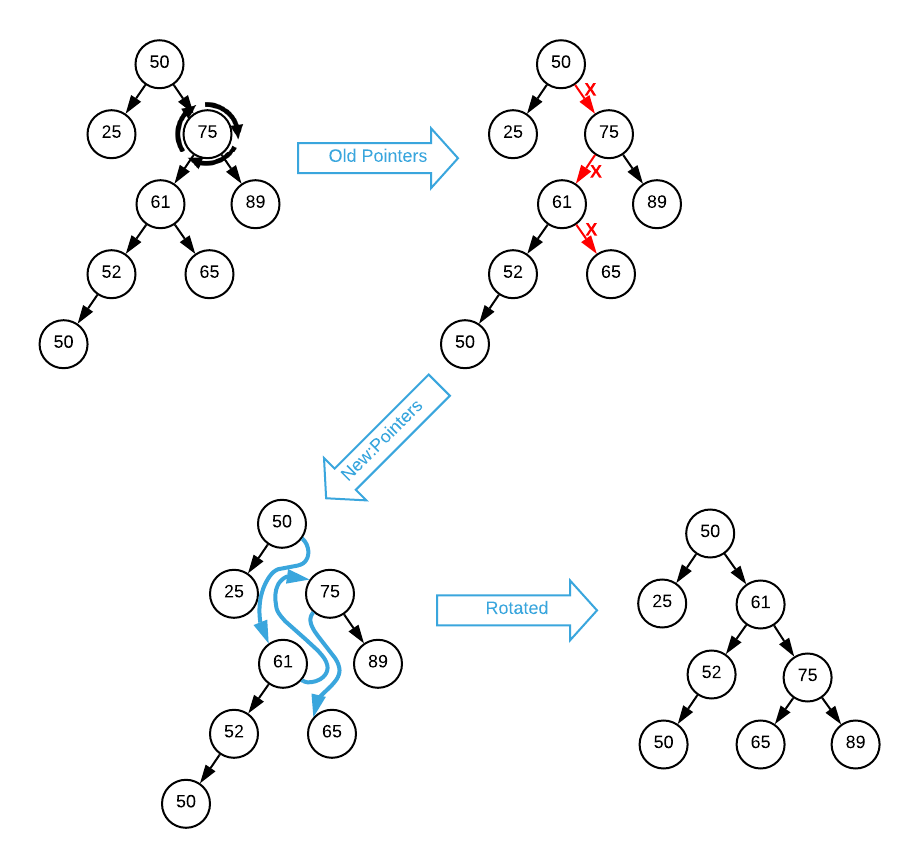
The steps for right rotation are similar to that of the left rotation.
- The parent (50) of the rotation node (75) becomes the parent of the left node (61).
- The rotation node’s (75) left pointer is updated to the left node’s right pointer (NULL)
- The left node’s (61) right pointer changes to the rotation node (75)
Self balancing isn’t entirely intuitive and it takes time to internalize the concept. The reader is highly encouraged to master rotations before advancing as it is assumed knowledge in the next section on red-black trees. As previously stated, a though treatment of self-balancing implementations is out of scope, However, red-black trees are a representative sample of self balancing implementations. They are popular and the concepts are easily translatable to other tree variations.
Exercises
-
Assuming you have a binary search tree with 1074 nodes, what is height given:
a. A self-balancing tree having items inserted in sequential order
b. A non-self-balancing tree having items inserted in random order
c. A non-self-balancing tree having items inserted in sequential orderAnswers (click to expand)
- The tree will remain balanced so the height is $\log_{2}1074 \approx10.06877$ which rounds up to $11$.
- Inserting nodes in random order statitically produces a balanced tree. The height will be close to $\log_{2}1074 \approx10.06877$ which rounds up to $11$.
- Inserting items sequentially with no balancing mechanism produces a tree where all the left or right pointers are NULL. The height is equal to the number of nodes, in this case 1074.
-
Calculate the height of a non-self-balancing binary search tree of integers given that nodes are inserted in the order specified below. The first node added to the tree becomes the root.
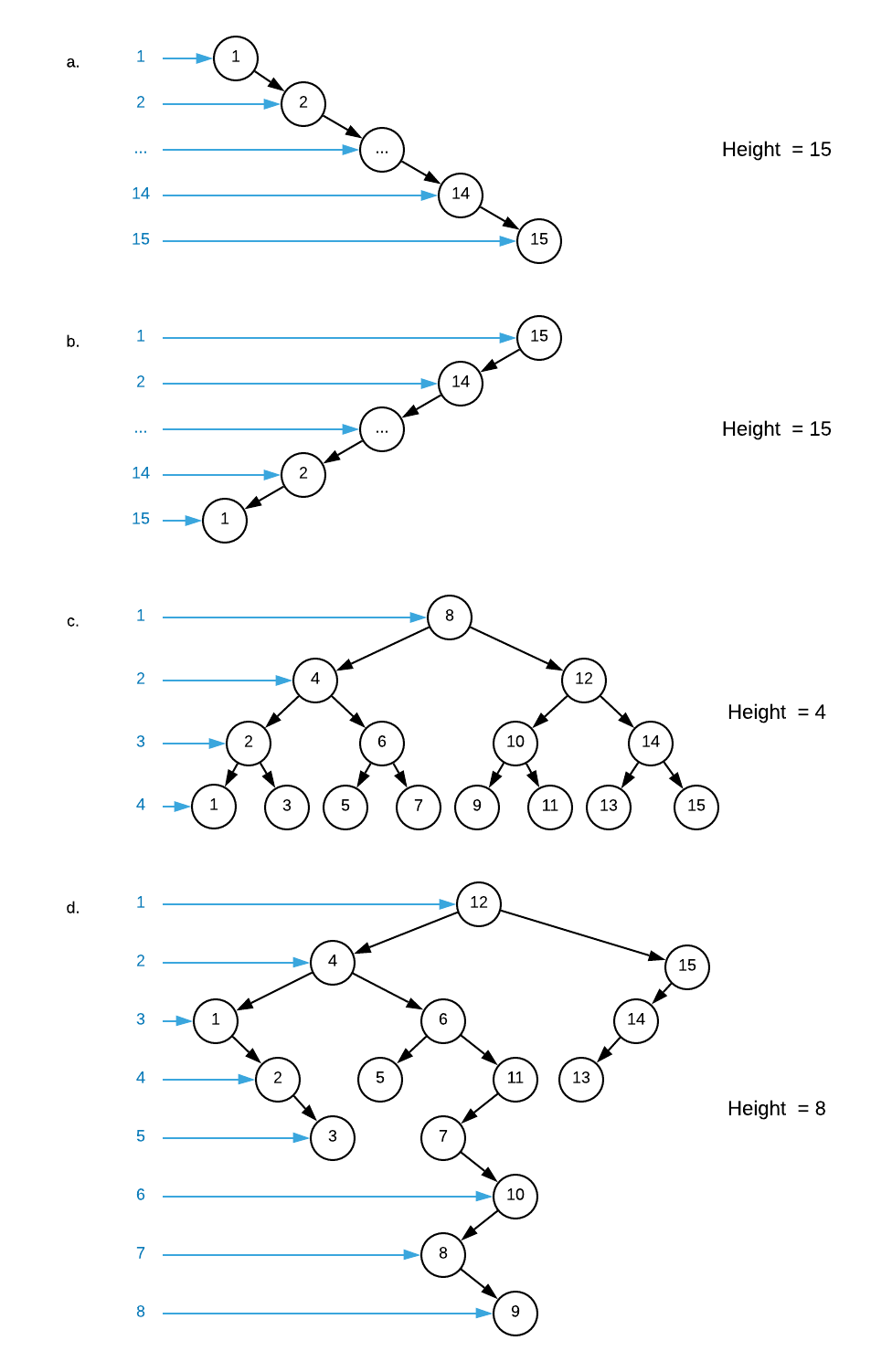
a. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
b. 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
c. 8, 4, 2, 1, 3, 6, 5, 7, 12, 10, 9, 11, 14, 13, 15
d. 12, 4, 1, 2, 3, 6, 5, 11, 7, 10, 8, 9, 15, 14, 13Answers (click to expand)
-
Starting with the binary search tree of integers depicted in the image below, describe a single rotation operation that will reduce the tree’s height to 3.
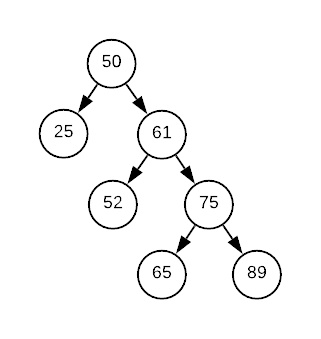
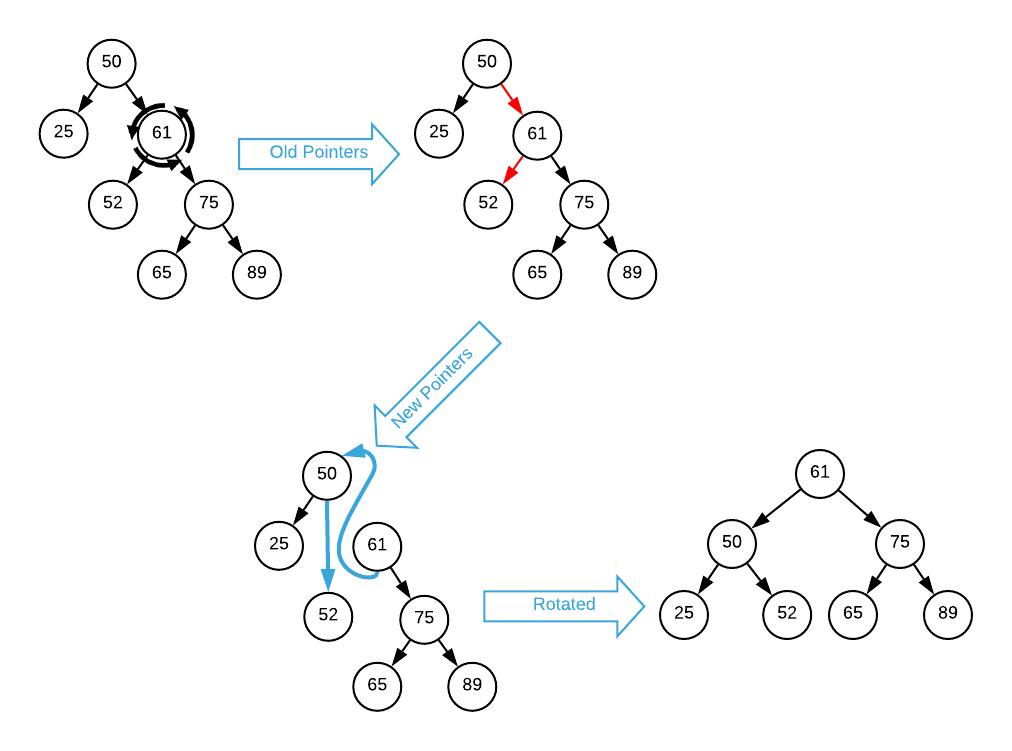
Answers (click to expand)
Left rotate the 61 node.
-
Define pseudo code for both a left and right binary tree node rotation. Assume the functions accept an existing binary tree node and the binary tree is tracking parent pointers89.
For formatting purposes, the answers for question 4 are located here.
-
More accurately, it’s not possible to reduce the height of a balanced tree. This concept is explained in the succeeding section. ↩
-
Available online at https://zhjwpku.com/assets/pdf/AED2-10-avl-paper.pdf ↩
-
For example, implementing a database. ↩
-
Recall the Principal of Parsimony ↩
-
Many self-balancing trees only add only constant time to insert and delete operations rending an identical asymptotic complexity. However, recall from Real World Asymptotic Complexity that constants do matter. Evaluate your use case carefully to determine if it matters for your particular context. ↩
-
Assuming a uniform distribution ↩
-
Depending on the implementation, parent nodes may also need to be rewired along with the pointer that specifies root. ↩
-
The purpose of parent pointers is explained on the Binary Tree page. This exercise is meant to reinforce that knowledge. ↩
-
Don’t fret if the answer isn’t entirely obvious; a neophyte can expect to invest upwards of three hours in a complete solution. This is by design. The only way to fully comprehend rotations is via experimentation and contemplation. A mountain of prose wont make the concept any more clear.
Many find it helpful to draw a visual representation of the operation before specifying pseudo code. Instead of starting from scratch, try adding parent pointers to the supplied drawings. ↩