Prerequisites (click to view)
graph LR
ALG(["fas:fa-trophy Queue fas:fa-trophy #160;"])
ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
click ASY_ANA "./math-asymptotic-analysis"
STACK(["fas:fa-check Stack #160;"])
click STACK "./data-struct-stack"
ASY_ANA-->ALG
STACK-->ALG
A queue, aka First-In-First-Out (FIFO) list, is almost identical to a Stack with the exception that items are removed in reverse order. Their primary purpose is to track a linear list of items in last-in-first-out order. Think of a queue like a line to get into a night club. New people are added to the end of the queue and people are removed from the front of the queue as they are let in to enjoy a night of dancing.
History
Similar to stack data structures, the origin of queues is difficult to determine. The concept has existed for many years. Accountants have used FIFO data for managing inventory since the 1800s1. Unfortunately, a literature search yielded no insight into the first use in a computer science context. It’s fair to say that a queue is a small adaption of a stack and the history of both are intertwined.
Queues have two primary operations: enqueue and dequeue2. They
are outlined in the Pseudo Code section, take a minute to read
them over. The image below depicts queue operations graphically3.
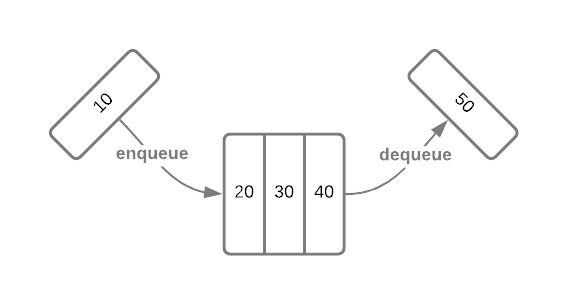
To solidify the concept, consider a queue of character data. The image below depicts a series of operations.
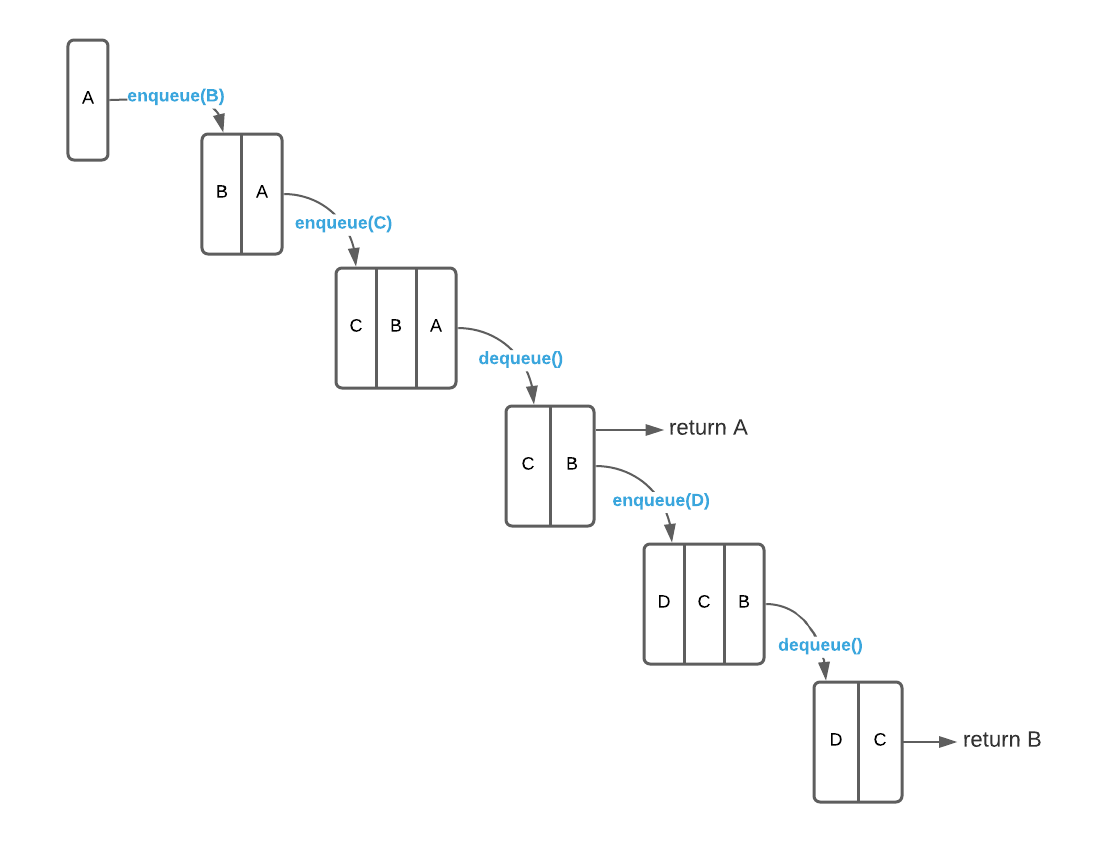
There are several viable ways to implement a queue. The most popular option for non-memory constrained applications is a linked list due to its simplicity. When memory is at a premium, circular queues are an excellent alternative.
Circular Queue
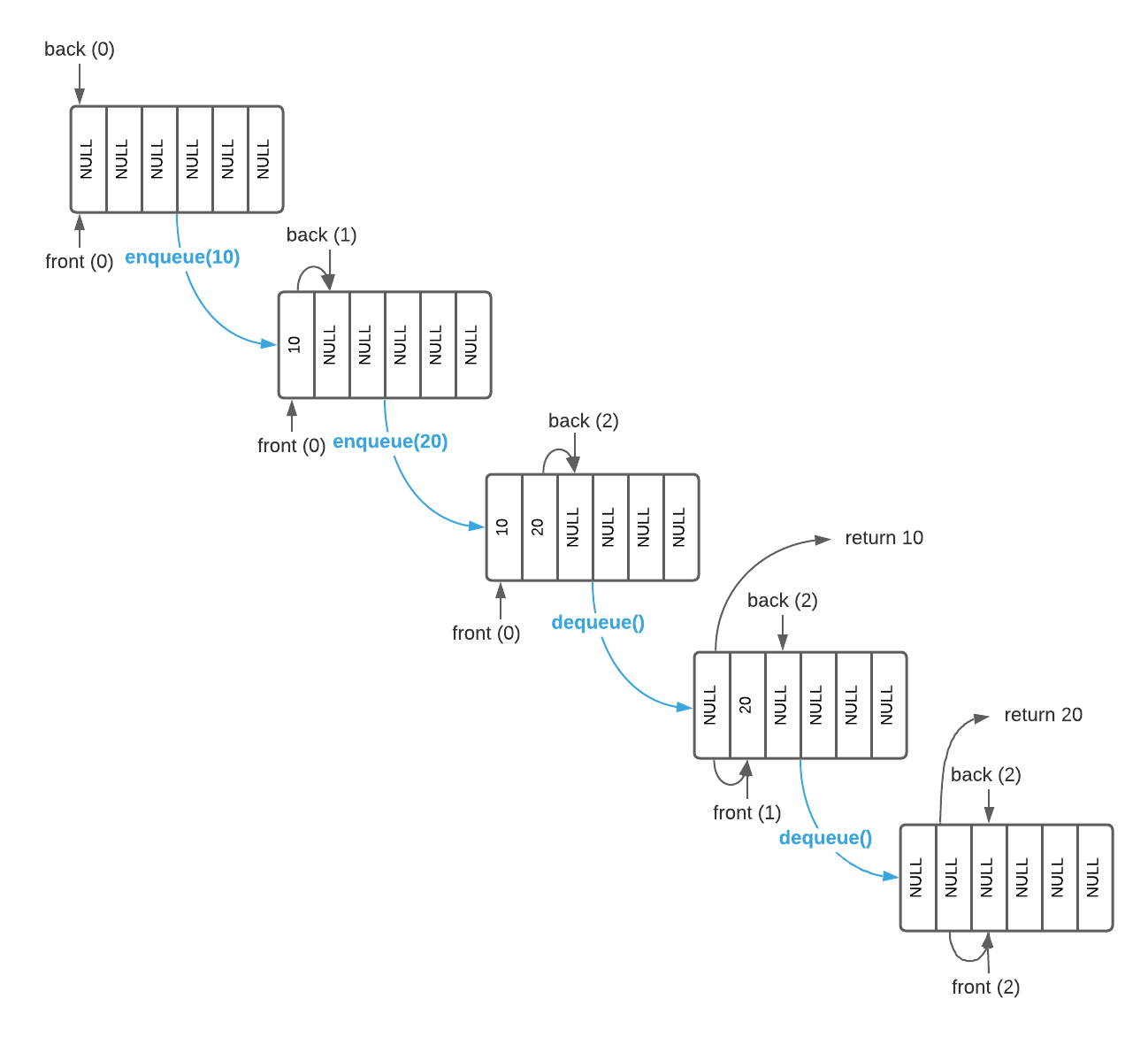
A circular queue, aka ring buffer, stores data in a fixed length array and
tracks mutable front and back4 indices. New items are added to
the front of the queue while items are removed from the back. The enqueue
operation stores an item at the back index and increments it. The dequeue
operation returns the item at the front index and increments it. This is a bit
more clear with an example. Consider the circular queue of integers depicted
below. As illustrated, the back pointer advances with each enqueue operation
while the front pointer advances with each dequeue operation.
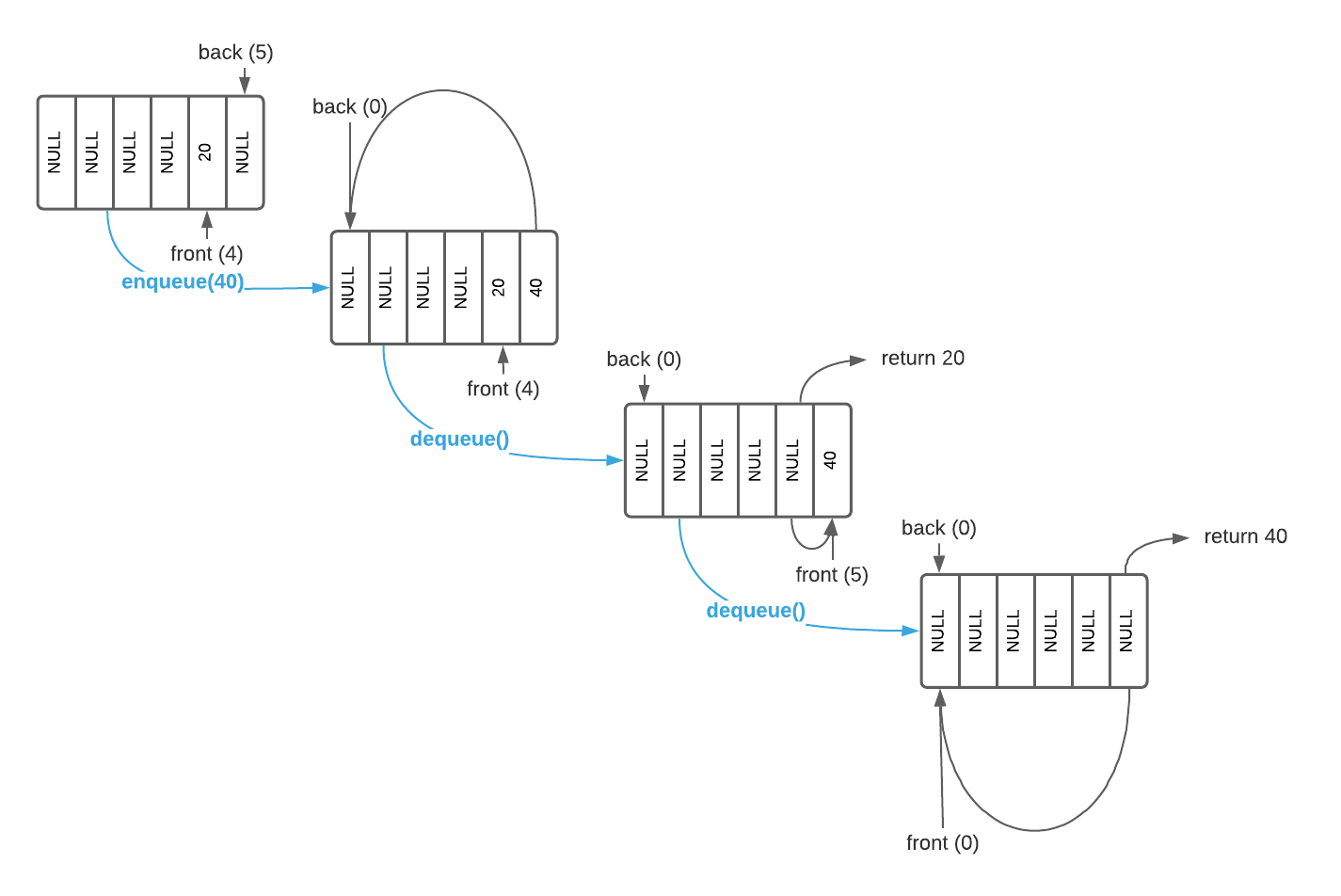
The next obvious question is, what happens when an index reaches the array bound. The answer is that it simply circles back to front. The image below illustrates this.
There is one more queue variation worthy of mention: deque.
Deque
As review, a stack always returns the newest item first (LIFO) and a queue always returns the oldest item first (FIFO). There is a another type of linear list data structure that combines the functionality of both: a double ended queue, commonly known as a deque. A deque is capable of adding and removing items from either side of the queue.
Unfortunately, there isn’t a strong naming convention around deque operations.
For the purposes of this article, assume the names push, push_right, pop,
and pop_right. The logic of each operation is depicted in the image below.
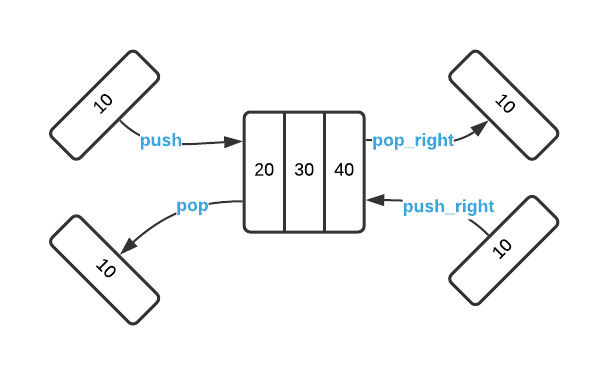
A deque is a good general purpose data structure. In spite of the added complexity, they are a great option for general purpose utilities.
Applications
- Job Scheduling: A print driver maintains a queue of print jobs and sends them to the printer as it is available.
- Buffering: Streaming video and audio applications typically maintain a buffer of content to compensate for erratic connections.
- Graph Breadth First Search
Pseudo Code
\begin{algorithm}
\caption{Queue Abstract Interface}
\begin{algorithmic}
\REQUIRE value = value to add to the queue
\FUNCTION{enqueue}{value}
\STATE add value to back of Q
\ENDFUNCTION
\FUNCTION{dequeue}{}
\STATE value $\gets$ front of queue
\STATE Q $\gets$ Q - value
\RETURN value
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
Implementation Details
Queue items are not required to to be the same size. If each item stores its size, it’s possible to advance the front/back pointers by a variable amount. The same is true for the stack data structure.
Asymptotic Complexity
- Enqueue: $O(1)$
- Dequeue: $O(1)$
Source Code
Relevant Files:
Click here for build and run instructions
Exercises
-
Consult the supplied Pseudo Code to answer this question. With the assumption that you are starting with a well formed empty queue capable of tracking integer values, list the items that exist on the queue after the following operations:
a.enqueue(55); enqueue(45); dequeue(); enqueue(65);
b.enqueue(1); enqueue(3); enqueue(8);
c.enqueue(75); enqueue(85); dequeue();
d.enqueue(100); dequeue(); enqueue(200); dequeue();Answers (click to expand)
-
65
45 -
8
3
1 - 85
- empty
-
65
-
Consider the pseudo code at the bottom of the page which specifies a dequeue implementation for a circular queue. Ignore bounds exceptions for the purposes of this question.
a. What would be the result of removing line 3?
b. What is the purpose of themod5 operation on line 4?Answers (click to expand)
- Removing line 3 has no effect on the algorithm. Enqueue operations will simply overwrite old values.
-
The `mod` operation is responsible for wrapping the index
to the top at the array bound. Assuming you have an array
of size 5:
0 mod 5 = 0
1 mod 5 = 1
2 mod 5 = 2
3 mod 5 = 3
4 mod 5 = 4
5 mod 5 = 0
-
Specify detailed pseudo code for a:
a. Circular queue
b. Deque
c. Queue implemented using two stacks6For formatting purposes, the answers to question 3 are located here.
\begin{algorithm}
\caption{Queue - Question 2}
\begin{algorithmic}
\FUNCTION{dequeue}{}
\STATE value $\gets$ array[front]
\STATE array[front] = NULL
\STATE front $\gets$ (back + 1) $\bmod$ array size
\RETURN{value}
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
-
See the online article History of LIFO for a fascinating historical account. ↩
-
It’s common to encounter additional operations. These two represent the minimal viable interface. ↩
-
One might notice that stacks were depicted vertically and queues are depicted horizontally. The difference is purely logical. Each square in the picture represents a block of memory and there is no relationship between the shape and actual memory location. ↩
-
Sometimes referred to as head and tail. ↩
-
\[3 \bmod 2 = \require{enclose} \begin{array}{rll} 1 \\ 2 \enclose{longdiv}{3}\kern-.2ex \\ \underline{- 2}\\ \term{1} \end{array} = 1\]modis short for modulo which indicates modular arithmetic. A detailed description of the concept is beyond the scope of this course. It’s sufficient to understand that $x \bmod y$ returns the remainder of $\frac{x}{y}$. See the example below: -
This is an exercise to test your understanding of stacks and queues. You should never use a structure such as this in a real world scenario. ↩