Prerequisites (click to view)
graph LR
ALG(["fas:fa-trophy Red Black Tree fas:fa-trophy #160;"])
ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
click ASY_ANA "./math-asymptotic-analysis"
BT(["fas:fa-check Binary Tree #160;"])
click BT "./list-data-struct-binary-tree"
SBT(["fas:fa-check Self Balancing Binary Tree #160;"])
click SBT "./list-data-struct-self-bal-tree"
ASY_ANA-->ALG
BT-->SBT-->ALG
Red-black trees are one of the many strains of Self Balancing Binary Trees. It’s not practical to cover all variations owing to the breadth of topic. However, red-black balancing techniques are representative of the whole. A conception of this data structure will equip one with the mental tools necessary to pursue other alternatives.
A red-black tree is an enhanced binary search tree designed to approximately minimize the height of the tree. The changes required to transform a binary search tree into a red-black tree are strictly additive. That is to say, a red-black tree is a standard binary search tree that maintains additional invariants. Before diving into these invariants, it’s prudent to define what the colors red and black denote.
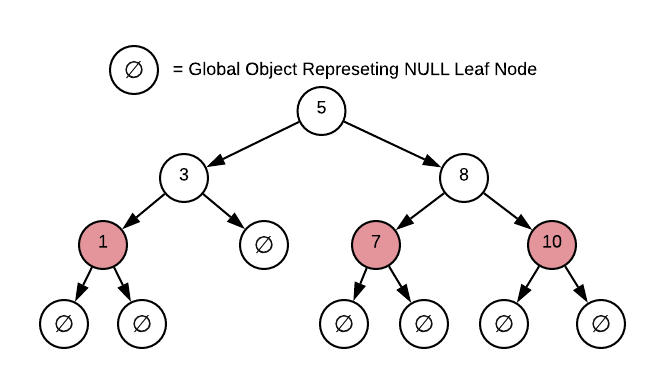
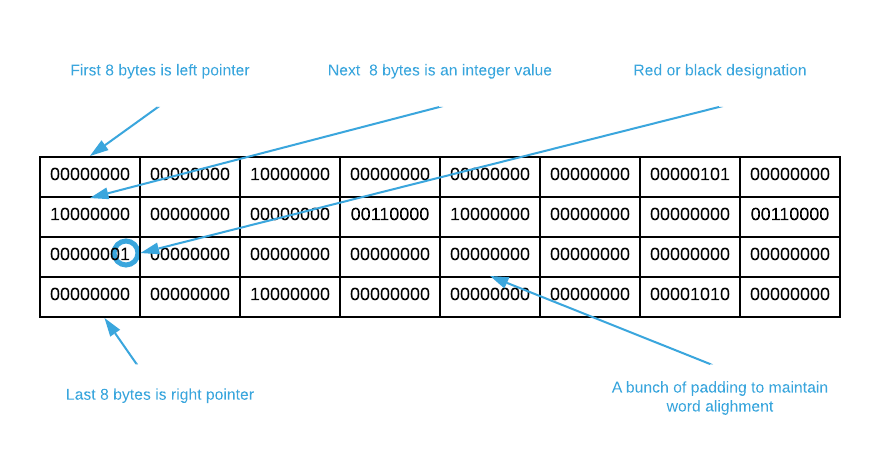
As one might infer from the name, every red-black tree node has a red or black color designation. This is often confusing upon first encounter because it’s nonsensical to literally color a tree node. However, red or black is nothing more than a binary state designation1. It’s possible to replace red with pirate and black with ninja and achieve the same result. The intent is to store a bit on every node indicating one of two possible states. To solidify this concept, the image below illustrates the memory layout of a node from a red-black tree of 64-bit integers2.
History
The Xerox PARC company is famous for many groundbreaking inventions3, the most notable of which is the Graphical User Interface (GUI). It’s not surprising that many algorithms also find their origins there. Two Xerox employees, Robert Sedgewick and Leonidas J. Guibas, published a paper in 1978 entitled A Dichromatic Framework for Balanced Trees4 which introduced red-black trees to the world. To borrow an aphorism from Issac Newton, Sedgewick an Guibas were “standing on the shoulders of giants”. They attribute much of their work to Rudolf Bayer’s 1972 paper entitled Symmetric binary B-Trees: Data structure and maintenance algorithms5.
Red-Black Invariants
As mentioned above, a red-black tree is a standard binary search tree that maintains additional invariants, four to be exact. They are listed below.
- Every node is designated as either red or black
- The root node is always black
- Red nodes must have black children and parents6
- Every path starting at the root node and ending in a
NULLpointer7 must pass through the same number of black nodes
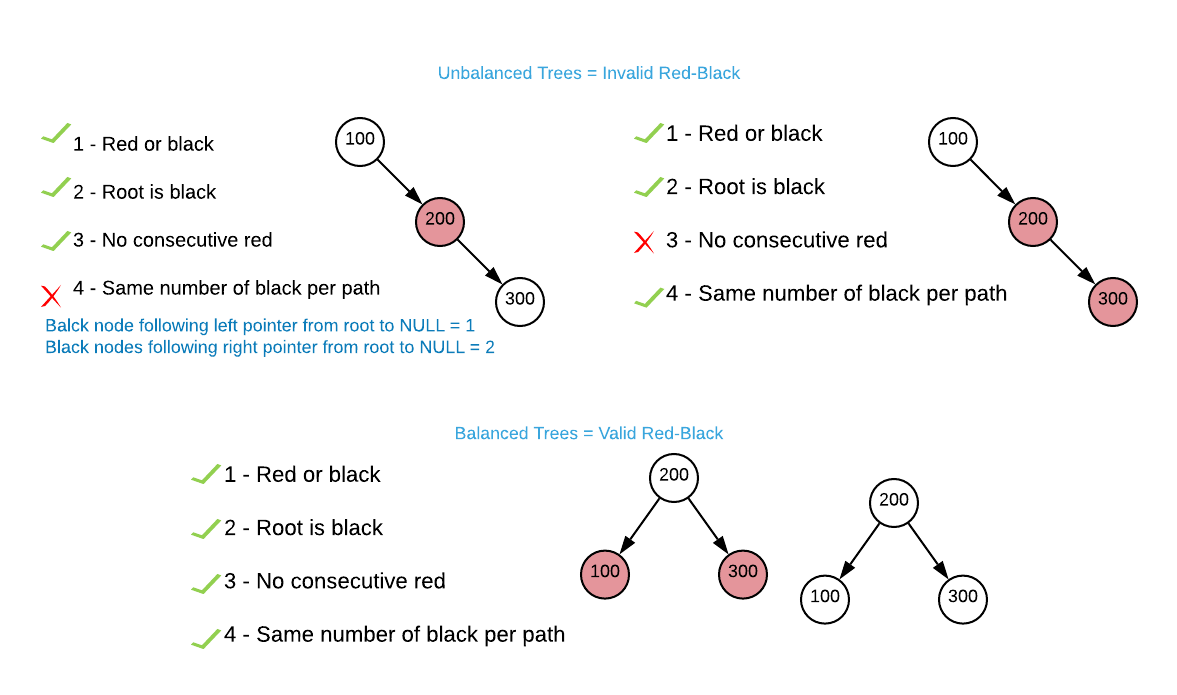
It’s not entirely obvious how maintaining these invariants minimizes tree height. Consider the simplest possible case: a tree with three nodes. It’s not possible to arrange the nodes in such a way that it is both unbalanced and also a valid red-black tree as illustrated below8.
Every insert/delete operation has the potential to invalidate the invariants; therefore, they must be evaluated and restored. The sections below outline the exact algorithms is more detail, but at a high level invariants are restored via a series of recolor and rotation procedures. As an example, consider the insert operation depicted below.

As the number of nodes increase, maintaining the invariants does NOT guarantee perfect balance. This may seems like a oversight but it’s actually a feature.
Close Enough Balance
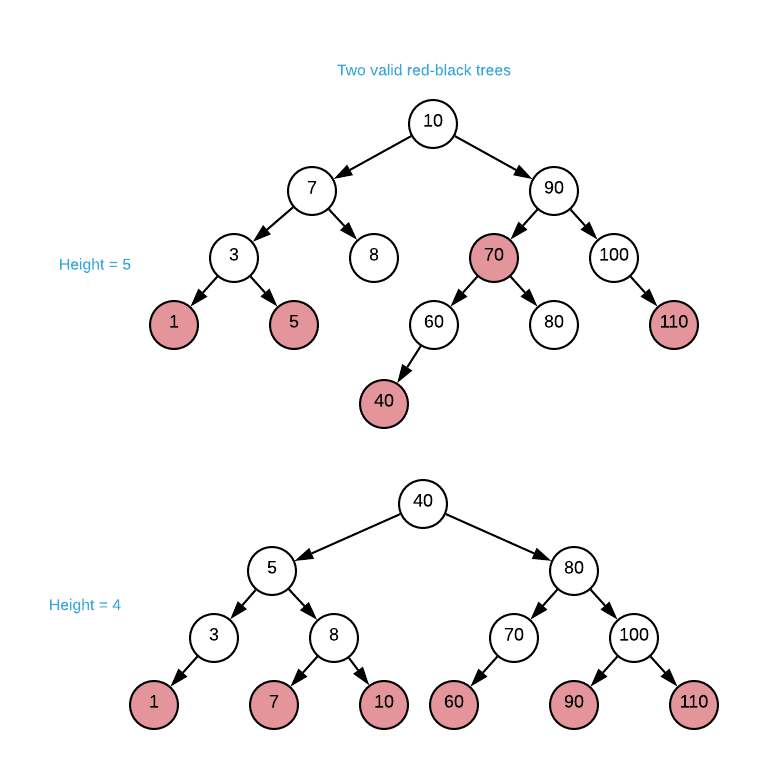
An interesting feature of red-black trees is that they do not attempt to maintain perfect balance. For instance, consider the two valid red-black trees depicted below. Both trees contain the exact same values and satisfy all invariants yet the bottom tree is more balanced than the top.
The relaxed balancing constraint results in slightly less efficient search operations and considerably more efficient insert/delete operations owning to fewer requite rotations. In practice, the search performance deficit in negligible. A perfectly balanced tree has $\text{height} = \log_2{n}$ while red-black trees guarantee $\text{height} \leq 2\log_2{n + 1}$. To provide a sense of the height difference, the table below compares the two functions.
| Tree size $n$ | $\log_2{n}$ | $2\log_2{n+1}$ |
|---|---|---|
| 10 | 4 | 7 |
| 100 | 7 | 14 |
| 1000 | 10 | 20 |
| 10000 | 14 | 27 |
| 100000 | 17 | 34 |
| 1000000 | 20 | 40 |
| 10000000 | 24 | 47 |
Stated a bit more intuitively, the maximum difference between the depth of any two leaves is one for a perfectly balanced tree and two for a red black tree. Next, we’ll examine an insert operation.
Insert Operations
One could examine the pseudo or source code to understand red-black tree insert operations. However, they are a bit abstruse without some additional commentary. At a high level, the insertion algorithm has four steps:
- Insert using the Binary Tree insert algorithm
- Color the new node red
- If the new node’s parent is black, no invariants are broken so terminate
- Restore red-black tree invariants
The first three steps are self-explanatory while the fourth is fairly complex; therefore, it is the focus for the remainder of this section. Restoring the red-black invariants is a recursive process starting at the inserted node. For each node the algorithm encounters, there are three possible scenarios:
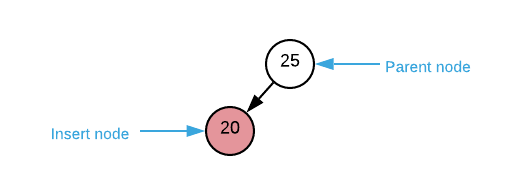
- The parent node is black
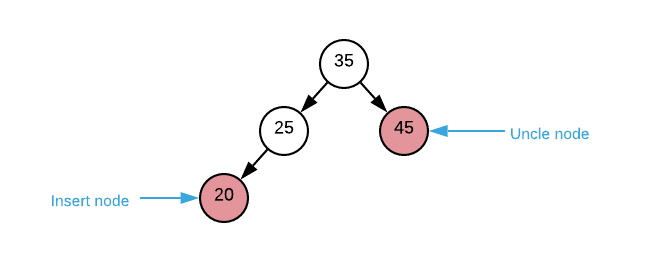
- The uncle node is red
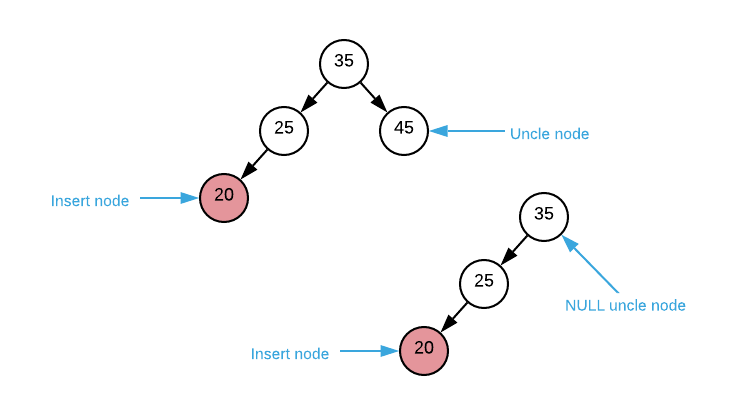
- The uncle node is black or
NULL
The actions taken for each scenario are outlined below.
- The parent node is black
- if root node is red, recolor it to black
- terminate
- The uncle node is red
- recolor parent node black
- recolor uncle node black
- recolor grandparent node red
- recurse on grandparent node
- The uncle node is black or
NULL- parent node is a left branch
- node is a right branch
- rotate parent left
- recurse on parent
- node is a left branch
- change parent node color to black
- change grandparent node color to red
- rotate grandparent node right
- recurse on node
- node is a right branch
- parent node is a right branch or
NULL- node is a left branch
- rotate parent node right
- recurse on parent node
- node is a right branch
- change parent node color to black
- change grandparent node color to red
- rotate grandparent node left
- recurse on node
- node is a left branch
- parent node is a left branch
Don’t worry if this seems a bit overwhelming. It’s normal to review red-black tree insertions several times before comprehension sets in. It’s also difficult to fathom without concrete examples. The image below steps through the process graphically.
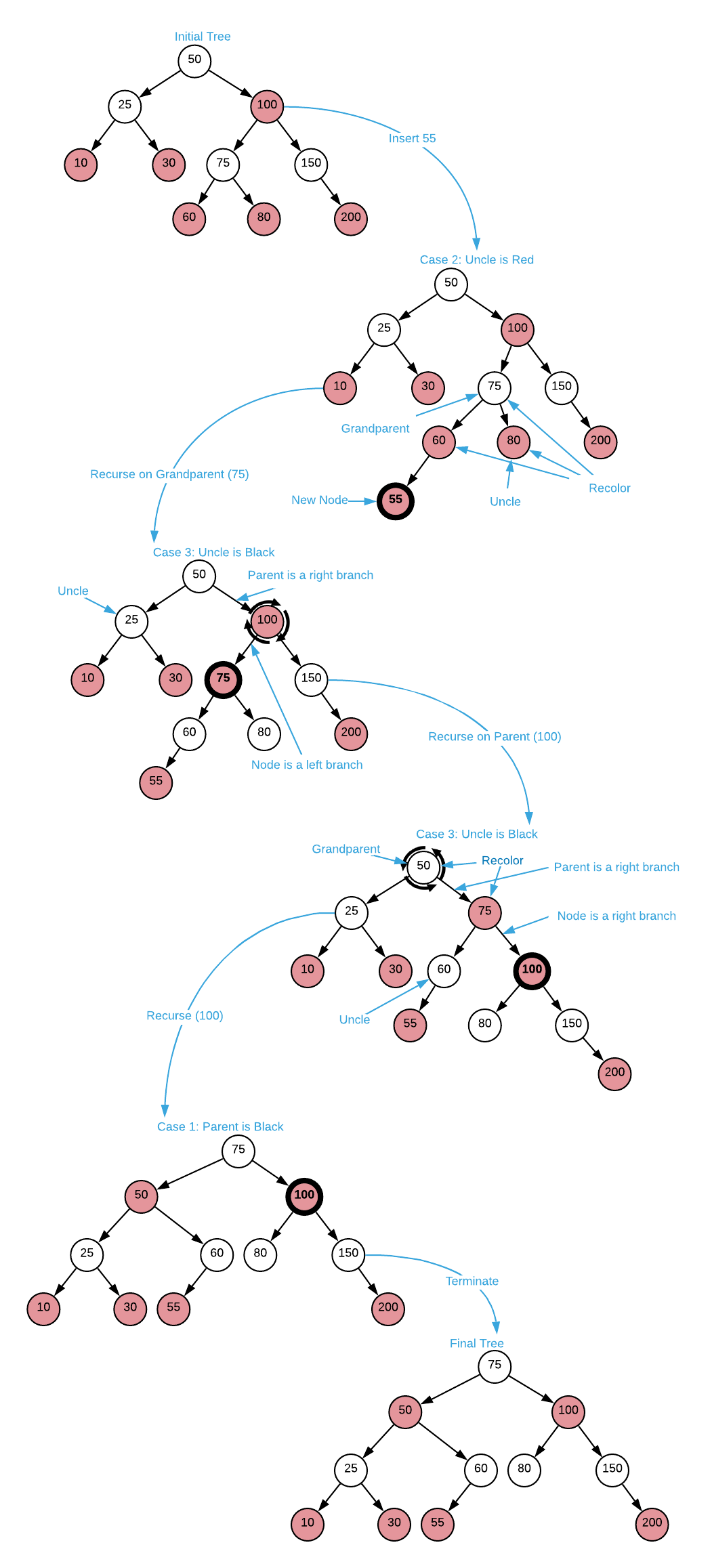
In order to keep these concepts as accessible as possible, a few arcane details were omitted. However, the pseudo code as well as accompanying source code are rigorously complete and should be studied assiduously. With a firm conceptual understanding, the code should be much more accessible.
Applications
A red-black tree is direct replacement for any standard binary search tree; therefore, they have the same applications. Below are a few notable instances of red-black trees.
- The Linux Completely Fair Scheduler (CFS)
- C++ STL Class map
Pseudo Code
As mentioned above, the changes required to transform a binary search tree into a red-black tree are strictly additive. All of the binary tree pseudo code as well as the rotation pseudo code apply here and is not repeated. The additive code responsible for maintaining the invariants after an insert operation is shown below. The delete operation is an exercise.
\begin{algorithm}
\caption{Red-Black Tree}
\begin{algorithmic}
\REQUIRE T = red-black tree
\REQUIRE $\text{new_node}$ = node to insert into the tree
\REQUIRE $\text{NULL_NODE}$ = global variable representing a black leaf node (see implementation details)
\FUNCTION{insert}{T, $\text{new_node}$}
\STATE \CALL{binaryTreeInsert}{T, $\text{new_node}$}
\STATE $\text{new_node}$.left $\gets \text{NULL_NODE}$
\STATE $\text{new_node}$.right $\gets \text{NULL_NODE}$
\STATE $\text{new_node}$.color $\gets$ RED
\STATE
\STATE node $\gets \text{new_node}$
\WHILE{node.parent.color = RED}
\IF{node.parent = node.grandparent.left}
\STATE uncle $\gets$ node.grandparent.right
\IF{uncle.color = RED}
\STATE uncle.color $\gets$ BLACK
\STATE node.parent.color $\gets$ BLACK
\STATE node.grandparent.color $\gets$ RED
\STATE node $\gets$ node.grandparent
\ELSEIF{node = node.parent.right}
\STATE node $\gets$ node.parent
\STATE \CALL{rotateLeft}{node}
\ELSE
\STATE node.parent.color = BLACK
\STATE node.grandparent.color = RED
\STATE \CALL{rotateRight}{node.grandparent}
\ENDIF
\ELSE
\STATE uncle $\gets$ node.grandparent.left
\IF{uncle.color = RED}
\STATE uncle.color $\gets$ BLACK
\STATE node.parent.color $\gets$ BLACK
\STATE node.grandparent.color $\gets$ RED
\STATE node $\gets$ node.grandparent
\ELSEIF{node = node.parent.left}
\STATE node $\gets$ node.parent
\STATE \CALL{rotateRight}{node}
\ELSE
\STATE node.parent.color $\gets$ BLACK
\STATE node.grandparent.color $\gets$ RED
\STATE \CALL{rotateLeft}{node}
\ENDIF
\ENDIF
\ENDWHILE
\STATE
\STATE T.root.color $\gets$ BLACK
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
Implementation Details
Typically, trees terminate with a
NULLpointer. Replacing them with a BLACK node representing aNULLvalue simplifies the logic. Without this, every node reference (left, right, parent, grandparent, uncle) must have branches to accommodateNULLvalues. The pseudo code above, as well as the supplied source code, implement a fifth invariant: allNULLpointers are BLACK nodes.An added optimization is to create a single global
NULLnode to avoid re-allocating every requisiteNULLnode. This is depicted in the image below.
Asymptotic Complexity
Please refer to Binary Tree Asymptotic Complexity. The additive changes required to transform a binary tree to a red-black tree, while not free, do not change the asymptotic complexity. It’s common to question how is it that rebalancing does not increase the complexity of the insert operation. The balance algorithm is $O(\log_2{n})$. Adding this to the insert operation yields $O(\log_2{n} + \log_2{n})$ or more simply $O(2\log_2{n})$. Eliminating the constants results in $O(\log_2{n})$. The search operation is similar, while it’s technically $O(2\log_2{n + 1})$, removing the constants leave us with $O(\log_2{n})$.
Advantages
- Binary Tree: Because a red-black tree is essentially an enhanced binary tree, it has the same advantages.
- Search: Guaranteed to remain balanced regardless of insertion order.
Disadvantages
- Binary Tree: Because a red-black tree is essentially an enhanced binary tree, it has the same disadvantages.
- Complexity: Added complexity.
Source Code
Relevant Files:
Click here for build and run instructions
Exercises
-
Answer True or False for each of the following statements:
a. Red-black tree invariants ensure that a tree is perfectly balanced.
b. A binary tree can be transformed into a red-black without modifying existing code.
c. The colors red and black are intrinsic to the data structure.Answers (click to expand)
- False: Red-black trees invariants guarantee approximate balance where $\text{height} \leq 2\log_2{n + 1}$.
- True: The changes required to transform a binary tree to a red-black tree are strictly additive.
- False: Any binary state designation would suffice.
-
Identify the violated invariant, if any, in each of the following red-black trees.
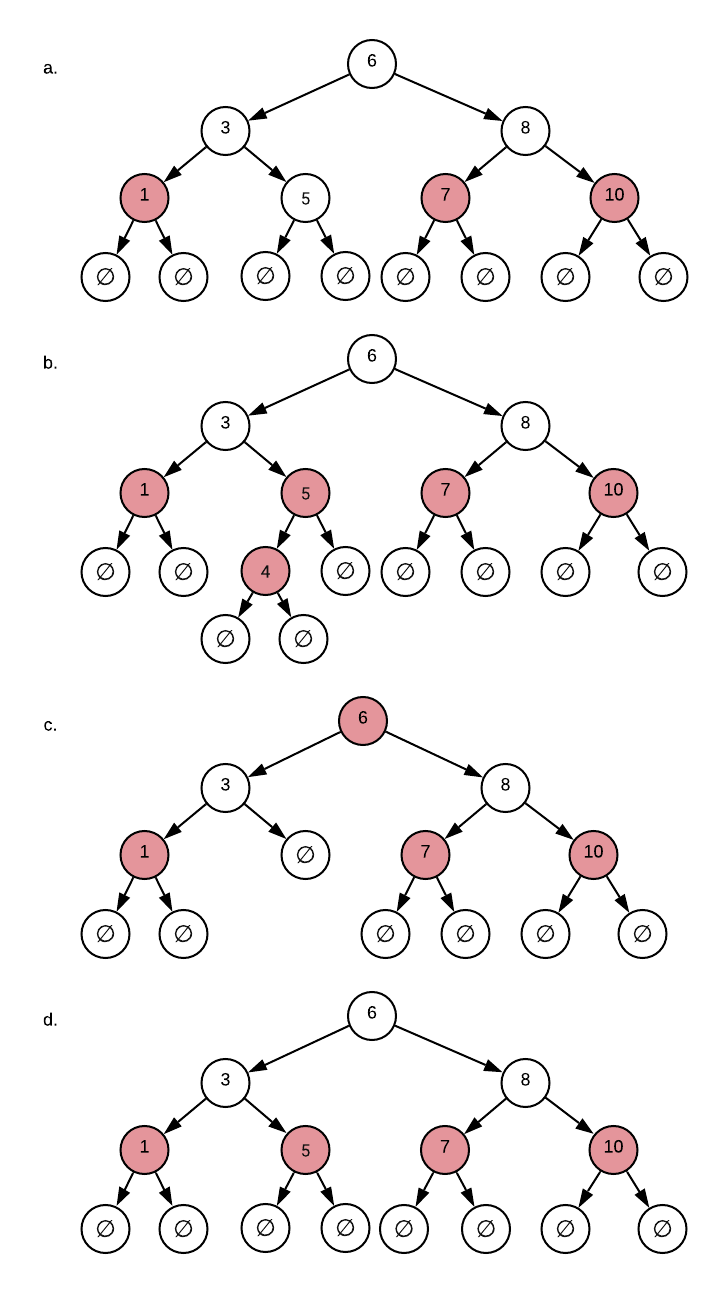
Answers (click to expand)
- The forth invariant, same number of black per path, is violated. There are three black nodes on the path from the `6` to the `5` while there are only two black nodes on every other path.
- The third invariant, no consecutive red nodes, is violated. `5` is a red node and it has a red child.
- The second invariant, root is black, is violated.
- There are no invariant violations: this is a valid red-black tree.
-
Specify the steps required to insert the value 40 into the red-black tree depicted below.
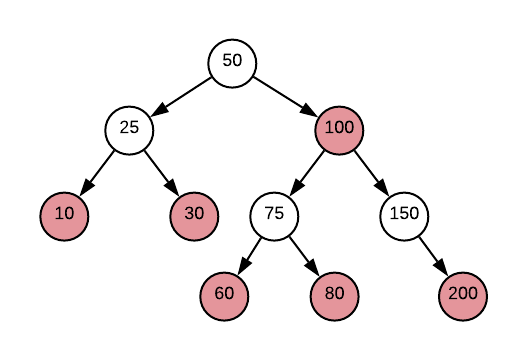
Answers (click to expand)
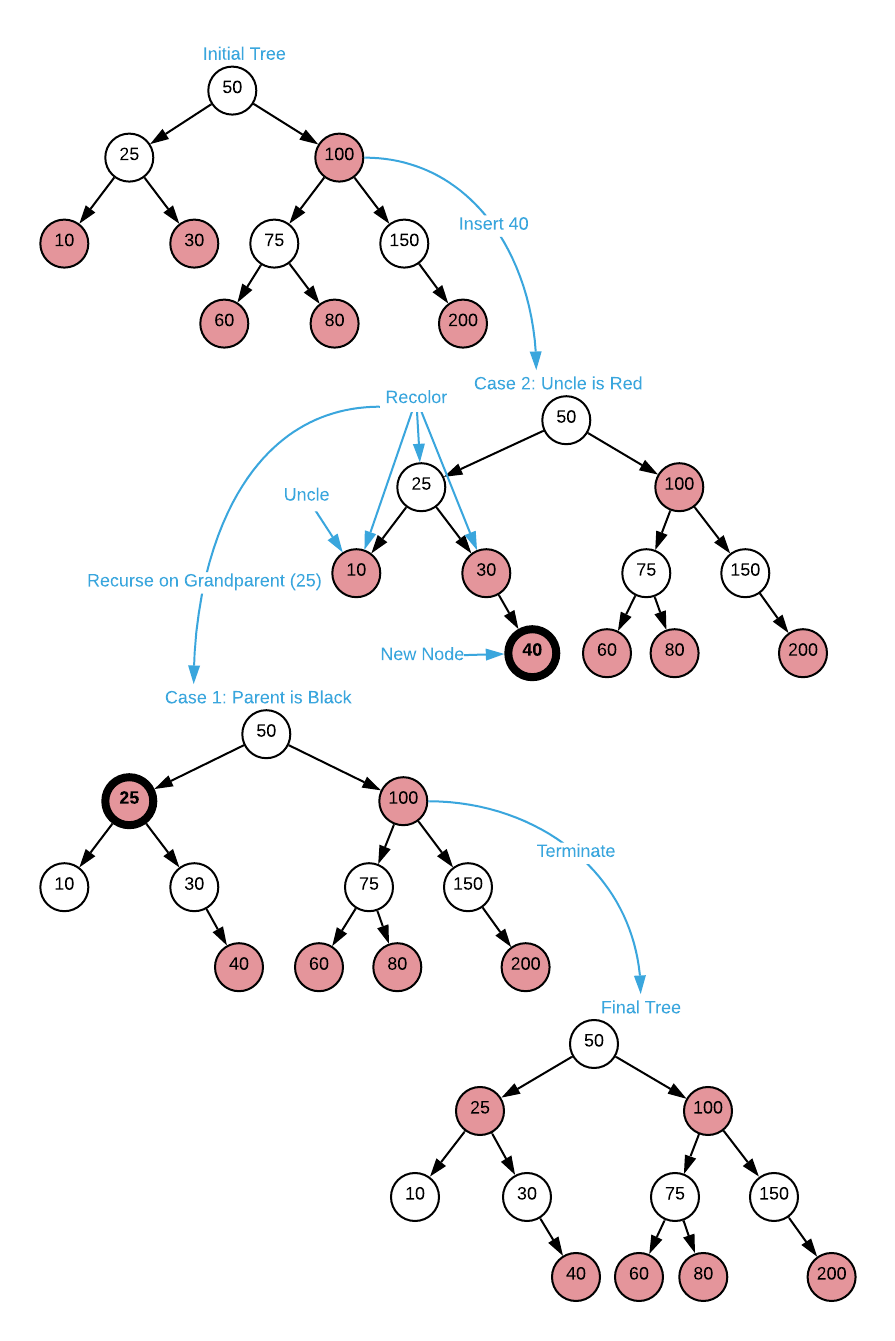
-
Specify the pseudo code for rebalancing a red-black tree after a delete operation9.
For formatting purposes, the answer to question 4 is located here.
-
The inventors, Robert Sedgewick and Leonidas J. Guibas, choose red and black to designate nodes for no other reason than that seventies-era printers produced ascetically pleasing prints using those colors. ↩
-
Modern machines optimize data structures by aligning values on word boundaries resulting in padding (sometimes referred to as slack) as illustrated in the graphic. While this consumes more space, it provides a notable speed optimization. The details are beyond the scope of this work. Please consult section 3.9.3 of Computer Systems: A Programmer’s Perspective (3rd Edition) by Randal E. Bryant and David R. O’Hallaron for a full treatment of the topic. ↩
-
…or discoveries depending on your philosophical predilection. Do scientific concepts exist before they are documented? If you believe they spring into existence in the human mind, then they are inventions. If you believe they are transcendent truths, they are discoveries. In practice, the distinction isn’t significant. ↩
-
Available online at https://ieeexplore.ieee.org/document/4567957 ↩
-
Available online at https://link.springer.com/article/10.1007%2FBF00289509 ↩
-
Otherwise stated, consecutive red nodes are prohibited. ↩
-
The path that traverse operations take through the tree when searching for a value not in the tree. ↩
-
The image does not provide an exhaustive account of every invalid variation, the reader is invited to extrapolate. ↩
-
This question is intentionally difficult. Do not be discouraged if you are unable to come up with a correct answer even after many hours. The intent is to force the reader into deep contemplation. This is the only way to truly master the content. As is typical in life, the journey is more valuable than reaching the destination. Be patient, and try to come up with a solution before looking at the answer. ↩