Strongly Connected Components (Directed)

Deciphering connected components in a directed graph is a bit more difficult than it is in undirected graphs. A strongly connected component is a subsection of a directed graph in which there is a directed path from every vertex to every other vertex. The rather convoluted graph below demonstrates the concept.

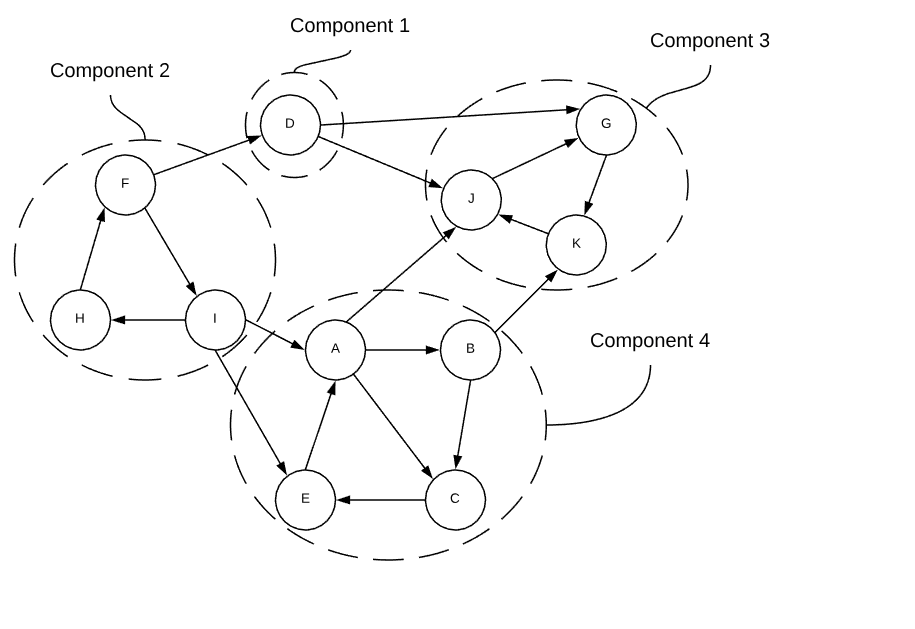
strongly connected components

If each strongly connected component is treated as a single node, the graph becomes a directed acyclic graph. Just like nodes in a directed graph, a strongly connected components with no incoming edges is known as a source and one without any outgoing edges is known as a sink.

Finding the strongly connected components of a directed graph is the most complex of the algorithms shown here. This algorithm (often referred to as the Kosaraju or Kosaraju-Sharir algorithm) performs DFS twice. The first time it derives an ordering in which to process the vertices that guarantees the second pass of DFS will start with a sink component. In other words, the goal is to identify the reverse topological ordering of all strongly connected components. The second discovers the strongly connected components.

Applications

Collapse a complicated graph into a more manageable graph.

Asymptotic Complexity

\(O(m + n)\)

Pseudo Code

strong-connected-components:
    G = input graph
    S = stack to hold ordering

    magic-ordering(G, S)
    set all vertices to NOT conquered

    while S is not empty:
        v = S->pop
        if v is NOT conquered:
            scc-dfs(G, v)
            
scc-dfs:
    G = input graph
    v = starting vertex
    scc_id = strongly connected component id to mark all vertices with
    side effects: marks all reachable vertices with a strongly connected
    component id

    s = new stack data structure
    s->push(v)

    while s is not empty:
        v = s->pop
        if v is NOT conquered:
            conquer(v)
            v->scc_id = scc_id
            for each edge in v:
                w = edge->head
                s->push(w)

// equivalent to a topological sort with the direction of the edges reversed
magic-ordering:
    G = input graph
    S = stack to hold ordering

    for every vertex in G:
        if vertex is NOT conquered:
            reverse-topo-sort(G, S, vertex)

reverse-topo-sort:
    G = input graph
    S = stack to hold ordering
    v = starting vertex
    side effect: places vertices on the stack in the "magic order"

    conquer(v)

    for each incoming edge in V:
        w = edge->tail
        if w is NOT conquered:
            reverse-topo-sort(G, S, w)

    S->push(v)

Source Code

Full Repo

Relevant Files:

Click here for build and run instructions