Bubble Sort

graph LR
	ALG(["fas:fa-trophy Bubble Sort fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	ARRAY(["fas:fa-check Array #160;"])
    click ARRAY "./list-data-struct-array"

	ASY_ANA-->ALG
	ARRAY-->ALG

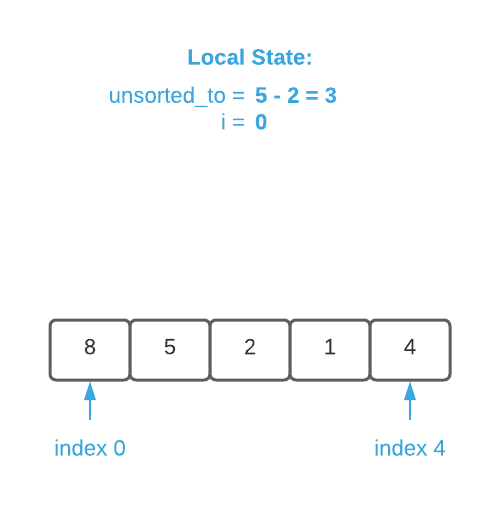
Bubble sort is an easy algorithm to implement; however, its runtime is quadratic ($O(n^2)$) so it’s not a particularly efficient algorithm. As the name implies, it starts at the beginning of the data and bubbles each element to its proper place. The animation below illustrates bubble sort on an integer array containing five items.

History

Bubble sort was originally referred to as “sorting by exchange”. It’s difficult to determine its exact origin because it was never regarded as an optimal choice for a general purpose sorting solution. The first mention of sorting by exchange is in a 1956 paper by Edward H. Fried entitled Sorting on Electronic Computer Systems¹. The paper offers up the algorithm as an example of an inefficient algorithm. Then, as today, its primary utility is pedagogical.

The paucity of prose here is intentional as it is not an effective tool for conveying algorithm details. The reader is encouraged to thoroughly peruse the pseudo code instead.

Pseudo Code

\begin{algorithm}
\caption{Bubble Sort}
\begin{algorithmic}
\REQUIRE $A$ = list of numbers where $\vert A \vert \gt 2$
\ENSURE $A$ sorted in sequential order
\FUNCTION{bubbleSort}{$A$}
    \STATE sorted $\gets$ false
    \STATE unsorted-to-index $\gets \vert A \vert - 2$
    \WHILE{sorted is false}
        \STATE sorted $\gets$ true
        \FOR{i $\gets$ 0 to unsorted-to-index}
            \IF{$A_i \gt A_{i+1}$}
                \STATE swap $A_i$ and $A_{i+1}$
                \STATE sorted $\gets$ false
            \ENDIF
        \ENDFOR
        \STATE usorted-to-index $\gets$ unsorted-to-index - 1
    \ENDWHILE
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Asymptotic Complexity

$O(n^2)$

Source Code

Full Repo

Relevant Files:

• bubble_sort.h
• bubble_sort.c
• bubble_sort_test.c

Click here for build and run instructions

Exercises

1. Assume line 4 of the bubble sort pseudo code is changed to:
   \(\text{for}\space j \in A \space\text{do}\)
   Specify $\Omega$ for the modified algorithm.

   Answers (click to expand)

   $\Omega(n^2)$ - There is no chance for the algorithm to stop early so the lower bound is the same as the upper bound. The modified algorithm becomes $\Theta(n^2)$.

2. Specify $\Omega$ for the bubble sort pseudo code algorithm.

   HINT: What happens in the case where the data is already in sorted order.

   Answers (click to expand)

   $\Omega(n)$ - If the data is already sorted, line 9 will never set the sorted variable to false. As such, line 4 will evaluate to false after iterating through the array once.

3. Using the programming language of your choice, implement a bubble sort function that accepts:
   • an array of any type
   • a sorting strategy
   Answers (click to expand)

   See the C implementation provided in the links below. Your implementation may vary significantly and still be correct.
   - bubble_sort.h
   - bubble_sort.c
   - bubble_sort_test.c

4. The sort.txt file contains one integer per line. Using the programming language of your choice, write a program that parses the file and places all the integers in an array. Next, using bubble sort, sort the array in the following order:
   • odd numbers in ascending order
   • even number is ascending order

   For instance, the numbers 3, 4, 8, 6, 9, 1 sort to 1, 3, 9, 4, 6, 8.

   Answers (click to expand)

   See the C implementation provided in bubble_sort_test.c Your implementation may vary significantly and still be correct.
   For reference, the first 10 sorted numbers are 1, 3, 5, 7, 9, 11, 13, 15, 17, and 19. The last 10 sorted numbers are 9982, 9984, 9986, 9988, 9990, 9992, 9994, 9996, 9998, and 10000.