Selection Sort

graph LR
	ALG(["fas:fa-trophy Selection Sort fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	ARRAY(["fas:fa-check Array #160;"])
    click ARRAY "./list-data-struct-array"

	ASY_ANA-->ALG
	ARRAY-->ALG

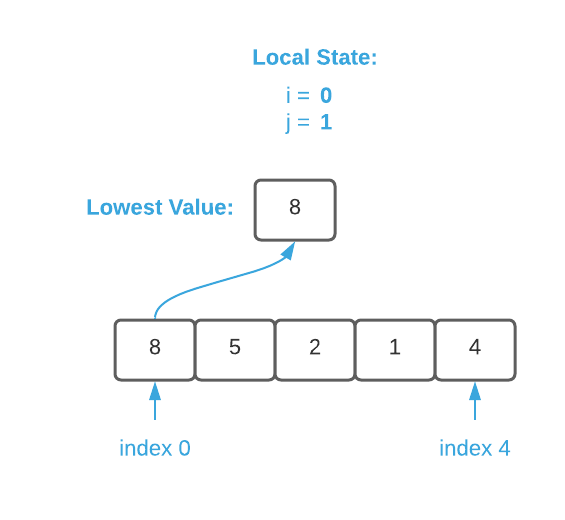
Selection sort is the last simplistic sorting algorithms covered here¹. It works by repeatedly searching for the next minimum value and moving it to the correct position. It’s difficult to describe with prose; however, it’s the easiest sorting algorithm to implement. Examine the animated image below in conjunction with the supplied pseudo code to understand it’s inner working.

Recall that bubble and insertion sort are $\Omega(n)-O(n^2)$ algorithms. When the data is pre-sorted the number of operations is linear to the input size. In the worst case scenario, reverse sorted data, the number of operations is $n^2$. Conversely, selection sort is $\Theta(n^2)$: the number of operations is the same regardless of the input data. One would assume that selection sort is inferior based on this data. However, recall that the RAM model weights all operations equally. The innovation of selection sort is that while the number of comparison operations is commiserate, the number of copy operation is minimized.

In this context, a copy is defined as copying data from one memory location to another. The pseudo code below demonstrates the three copy operations² associated with swapping two array values.

int temp;

temp = A[i]; // 1st copy
A[i] = A[j]; // 2nd copy
A[j] = temp; // 3rd copy

Selection sort may outperform other simplistic sort algorithms owing to fewer copy operations. This is an important attribute to keep in mind for situations where moving data is expensive.

Pseudo Code

\begin{algorithm}
\caption{Selection Sort}
\begin{algorithmic}
\REQUIRE $A$ = list of numbers
\ENSURE $A$ sorted in sequential order
\FUNCTION{selectionSort}{$A$}
    \FOR{i $\gets$ 0 to ($\vert A \vert$ - 1)}
        \STATE lowest $\gets$ i
        \STATE
        \FOR{j $\gets$ (i + 1) to ($\vert A \vert$ - 1)}
            \IF{$A_{\text{lowest}} \gt A_j$ }
                \STATE lowest $\gets$ j
            \ENDIF
        \ENDFOR
        \STATE
        \STATE swap $A_{\text{lowest}}$ and $A_i$
    \ENDFOR
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Asymptotic Complexity

$\Theta(n^2)$

Source Code

Full Repo

Relevant Files:

• selection_sort.h
• selection_sort.c
• selection_sort_test.c

Click here for build and run instructions

Exercises

1. Assume line 6 of the selection sort pseudo code is changed to:
   \(\text{if} \space A_{\text{lowest}} \lt A_j\)
   How does this change the final state?

   Answers (click to expand)

   The data will be sorted in descending order rather than ascending order.

2. Using the programming language of your choice, implement a selection sort function that accepts:
   • an array of any type
   • a sorting strategy
   Answers (click to expand)

   See the C implementation provided in the links below. Your implementation may vary significantly and still be correct.
   - selection_sort.h
   - selection_sort.c
   - selection_sort_test.c

3. At this point, you should have implemented bubble, insertion, and selection sort. Instrument each of your algorithms to calculate the total number of copy and comparison operations. Next, sort the data contained in the sort.txt file and determine the total number of copy and comparison for each algorithm.

   Answers (click to expand)

   See the C implementation provided in sort_implementation.c Your implementation may vary significantly and still be correct. The final output should be:

       Bubble Sort: copy = 71,844,390 comparisons = 49,988,559 total = 121,832,949
    Insertion Sort: copy = 23,968,128 comparisons = 23,958,117 total =  47,926,245
    Selection Sort: copy =     29,964 comparisons = 49,995,000 total =  50,024,964