Portions of a Graph are said to be connected when there is no way to separate the vertices without edges crossing between the parts. A common task is to identify all connected components of a graph. Consider the graph below, it is made up of three connected components.
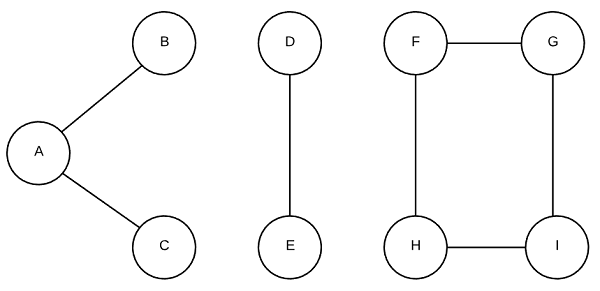
This algorithm identifies the connected components in a graph by marking each vertex with a component id. Any vertex with a matching id is part of the same connected component. Differing ids indicate no connectivity. Although shown below with BFS, DFS works equally well for this purpose.
Applications
- Connectivity - In a network, ensure that every node is reachable.
Asymptotic Complexity
\(O(m + n)\)
Pseudo Code
G = input graph
q = queue data structure
side effects: marks all vertices with a component id
component_id = 0
for each vertex (v) in G:
if v is NOT conquered:
component_id = component_id + 1
conquer(v)
v->component_id = component_id
q->enqueue(v)
while q is not empty:
v = q->dequeue
for each edge in v:
w = edge->head
if w is NOT conquered:
conquer(w)
w->component_id = component_id
q->enqueue(w)
Source Code
Relevant Files:
Click here for build and run instructions