Topological Ordering (Acyclic Directed)

A graph with no cycles is said to be acyclic. A directed acyclic graph is particularly interesting because such graphs have a least one (usually many) topological ordering. A graph with a cycle has no topological ordering. While the goal of this project is to abstain from recondite mathematical definitions, this concept is much easier to understand in such terms. A topological sort is an ordering of vertices $v_{1},v_{2},…v_{n}$ in such a way, that if there exists an edge with a tail of $v_{j}$ and a head of $v_{i}$, then $v_{j}$ comes before $v_{i}$. It’s a ordering of vertices in which the directed edges of the graph always move forward in the ordering. Consider a graph in which the vertices represent tasks and directed edges represent precedence constraints. The topological orderings are acceptable sequences in which to complete the tasks. This is depicted graphically below.

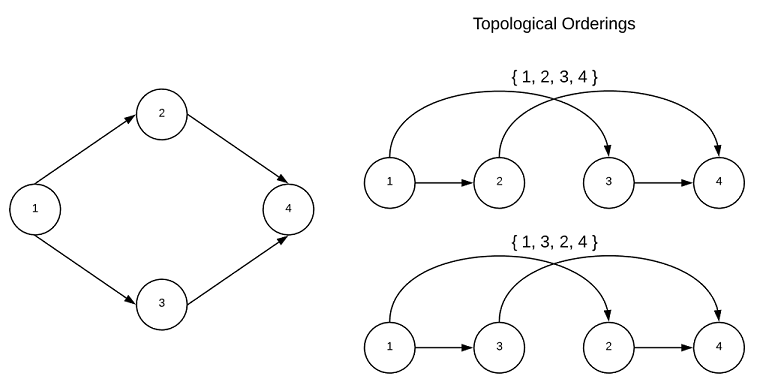
topological ordering

Every directed acyclic graph has a source vertex, that is a vertex with no incoming edges. Additionally, there must exists a vertex with no outgoing edges known as the sink vertex. The interested reader is encouraged to contemplate why this is true…

Just as some applications, such as shortest path, only work with BFS, topological ordering only works with DFS. The algorithm laid out below discovers a valid topological ordering for the input graph. One important thing to note is that this is only one of possibly many.

Applications

Determine the ideal order of tasks that have precedence constraints (e.g. university courses with pre-requisites or steps to solve a puzzle)

Asymptotic Complexity

$O(m + n)$

Pseudo Code

Global variable: order

topo-sort:
    G = input graph

    order = |V| - number of vertices in G
    for every vertex in G:
        if vertex is NOT conquered:
            dfs-topo(G, vertex)

dfs-topo:
    G = input graph
    v = starting vertex
    side effects: marks every vertex with a topological sort order

    conquer(v)

    for each edge in V:
        w = edge->head
        if w is NOT conquered:
            dfs-topo(G, w)

    v->top-order = order
    order = order - 1

Source Code

Full Repo

Relevant Files:

Click here for build and run instructions