Prerequisites (click to view)
graph LR
ALG(["fas:fa-trophy Bloom Filter fas:fa-trophy #160;"])
ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
click ASY_ANA "./math-asymptotic-analysis"
HT(["fas:fa-check Hash Table #160;"])
click HT "./data-struct-hash-table"
BW(["fas:fa-check Bitwise Logic #160;"])
click BW "./math-bitwise"
ASY_ANA-->ALG
BW-->ALG
HT-->ALG
A bloom filter is a particularly ingenious data structure whose purpose is to
efficiently determine set membership1 in constant time
($\Theta(1)$). The interface is analogous to a club membership roster. When a
person shows up at the clubhouse, the bouncer checks to see if their name is on
the roster. From the bouncer’s perspective, the roster is immutable. All they
can do is verify the existence of names. Similarly, the bloom filter abstract
interface has only two supported operations:insert(key) and lookup(key).
insert adds a key value to the set and lookup returns a boolean value
indicating if the key exists in the set. A particularly salient point is that
delete and get are not supported. Stated succinctly, bloom filters accept a
list of keys and “remember” them without the ability to retrieve, delete, or
enumerate them.
History
Burton Howard Bloom discovered bloom filters in 1970 while working at the Computer Usage Company in Newton Upper Falls, MA. He published a paper in the Communications of the ACM journal entitled Space/Time Trade-offs in Hash Coding Allowable Errors. It’s a “must read” for any software professional. The original intent was for database systems; however, bloom filters have become a staple for countless computing applications.
What’s extraordinary about bloom filters is that they are capable of determining set membership without actually storing the set’s constituent items. In fact, the data structure may consume as little as eight bytes of memory per item regardless of item size. This is accomplished by storing item hashes in such a way that several hashes are stored in a single memory location. See the image below2.
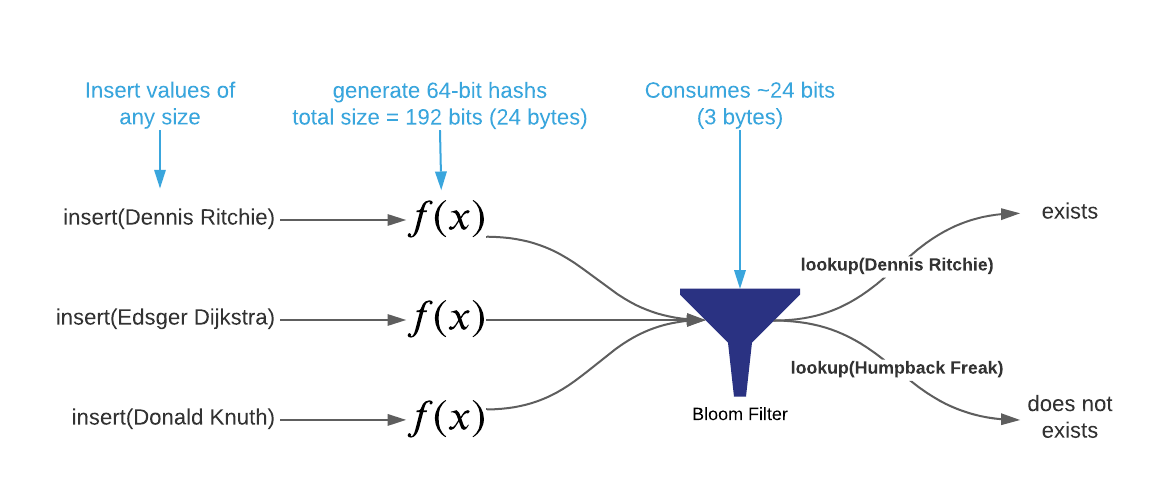
As portrayed to this point, bloom filters appear to be magic3. However,
there is, as always, a trade off and that trade off is accuracy. Bloom filters
are known as space-efficient probabilistic data structures. Such data
structures require engineers to balance error rate, memory space, and
performance to meet their specific needs. In the case of bloom filters, the
lookup operation has a probability of false-positive results. That is to say,
it may return exists given a key that was never inserted but it will never
return does not exist for a previously inserted key. Luckily, the error rate
is easily configurable via implementation parameters. This is examined in more
detail later on. First, we will explore the data structure’s internals.
Bloom Filter Internals
A bloom filter has two primary components:
- Collection of hash functions
- Bit vector4
When the insert operation accepts a key value, each hash function computes a
separate bit vector index5 from it. Next, the corresponding
bits in the vector are set to one. For example, consider a bloom filter that
holds a set of computer scientist names as portrayed in the image below.
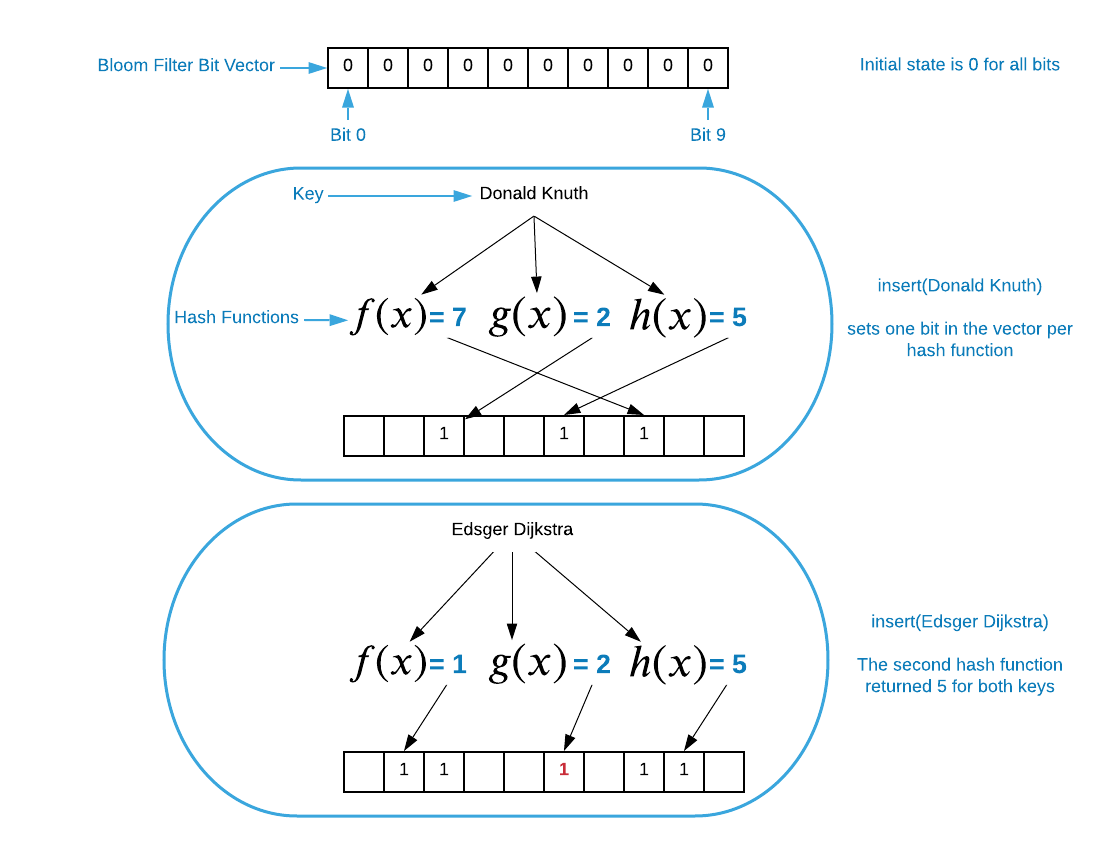
Notice the result of the insert operations. The first and second operations
set bit 5 to 1. This collision is
perfectly acceptable for bloom filters. The bit patterns are in essence stored
on top of one another. Examining lookup will demonstrate why this is true.
In a nutshell, lookup is simply the reverse of insert. When lookup accepts
a key value, each hash function computes a separate bit vector index from it.
Next, the algorithm examines the corresponding bits. If all of the bits have a
value of 1, return exists. Otherwise, return does not exist.
As mentioned above, bloom filters are probabilistic data structures, so
returning a definitive exists or does not exist is somewhat of a misnomer.
More accurate responses would be definite no and highly probable. Bloom
filters will never return does not exist for a key that was inserted. However,
false positives (exists for a key that was NOT inserted) are a probabilistic
possibility. This is depicted graphically below.
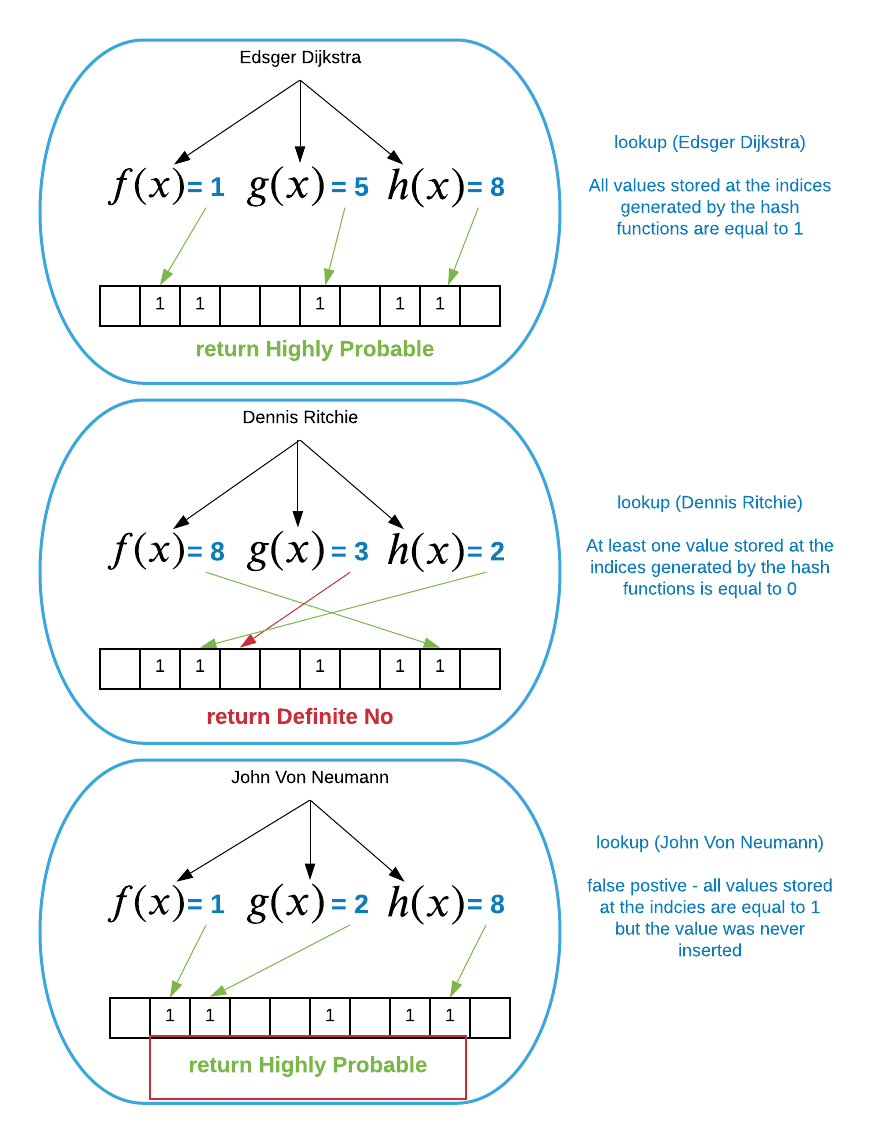
The name Edsger Dijkstra was inserted in the previous illustration, so it makes
sense that it returns a highly probable response. The names Dennis Ritchie and
John Von Neumann have not been inserted into the Bloom filter as of
yet6. Doing a look up on Dennis Ritchie results in definite no
because the second hash function returned a three and this bit is set to 0.
John Von Neumann demonstrates the dreaded false positive result. Even though the
name does not exist in the data structure, it returns highly probable because
all of the computed bits are set to one. The question now becomes, “just how
probable are false positives”.
Probability of False Positives
As alluded to earlier, it’s possible to tune the probability of false positives (error rate) by manipulating the number of hash functions (performance) and the length of the bit vector (memory space). Determining the correct balance for a specific context requires a straight forward calculation. The arcane details underlying the math are out of scope7. There are several perfectly suitable bloom filter calculators8 freely available on the internet for the time constrained.
The three equations below demonstrate the intrinsic relationship between error rate, memory consumption, and performance. $P$ is the probability of error, $m$ is the number of bits in the vector, $k$ is the number of hash functions, and $n$ is the number of items.
\[P=(1-[1-\frac{1}{m}]^{^{kn}})^k\] \[m=-\frac{n\ln P}{(\ln2)^2}\] \[k=\frac{m}{n}\ln 2\]As an example, assume you need to store $\blueci{50}$ items in a bloom filter with a probability of false positives to be no greater than 1% ($\greenci{.01}$). The size of the bit vector must be:
\[m=-\frac{\blueci{50}\ln \greenci{.01}}{(\ln2)^2}=479.252918868372\]Rounding the number of bits up to $\orangeci{480}$, the number of functions becomes:
\[k=\frac{\orangeci{480}}{\blueci{50}}\ln 2=6.6542129333755\]The final verdict is that in order to keep the probability of error under 1%, the bit vector must be at least 460 bits long and there must be at least 7 functions in the hash function list.
It should also be noted that all of the constraints and recommendations concerning hash functions outlined in the Hash Table section also apply here. It is assumed that each hash function is capable of simple uniform hashing and indices are also evenly distributed among them. Failing any of these requirements results in a higher error rate.
In conclusion, bloom filters are highly useful data structures for testing if objects belong to a pre-defined set. The constant time operations and comparatively meager memory space requirement make them highly practical. On the down side, they produce false positive results occasionally. Increasing space and performance consumption can reduce the error rate. Engineers should take special care to weigh the trade offs against the specific application’s needs.
Applications
- Forbidden Passwords: Storing forbidden passwords9 in a bloom filters provides an efficient means of validating new passwords. A false positive in this context is inconsequential.
- Recommendation Systems: Some websites suggest related content (blog posts, books, music, movies, etc..) based on the content that is currently being consumed. It is counter productive to suggest previously consumed content. A bloom filter offers a blazingly fast means of determining if suggestions are new to the user. The occasional false positive is inconsequential.
- Database Systems: Many databases such as Bigtable, HBase, Cassandra, and PostgreSQL use bloom filters to prevent superfluous lookups. In the event of a false positive, the algorithm simply performs a full search.
Asymptotic Complexity
- Insert: $\Theta(1)$
- Lookup: $\Theta(1)$
Pseudo Code
\begin{algorithm}
\caption{Bloom Filter Interface}
\begin{algorithmic}
\REQUIRE m = number of bits
\REQUIRE funcs = collection of hash functions
\OUTPUT bloom filter data structure
\FUNCTION{create}{m, funcs}
\STATE BF $\gets$ new memory allocation
\STATE BF.data $\gets$ bit vector of size m
\STATE BF.funcs $\gets$ funcs
\RETURN{BF}
\ENDFUNCTION
\STATE
\REQUIRE BF = bloom filter data structure
\REQUIRE key = arbitrary key value
\FUNCTION{insert}{BF, key}
\FOR{func $\in$ BF.funcs}
\STATE index $\gets$ \CALL{func}{key}
\STATE BF.data[index] $\gets$ 1
\ENDFOR
\ENDFUNCTION
\STATE
\REQUIRE BF = bloom filter data structure
\REQUIRE key = arbitrary key value
\FUNCTION{lookup}{BF, key}
\FOR{func $\in$ BF.funcs}
\STATE index $\gets$ \CALL{func}{key}
\IF{BF.data[index] = 0}
\RETURN definite no
\ENDIF
\ENDFOR
\RETURN highly probable
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
Implementation Details
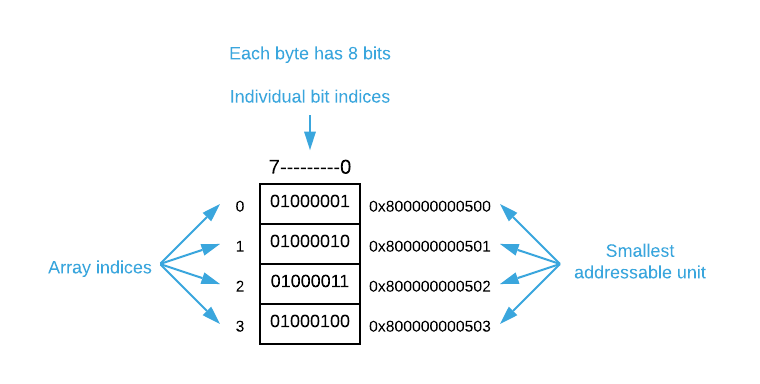
The pseudo code takes a few liberties with bit vectors. Unless you have a high-level language with a pre-defined bit vector, it’s not possible to refer to individual bits by index. The smallest addressable unit of memory is a byte which is comprised of 8 bits. You must use bitwise logic to manipulate individual bits.
To demonstrate, consider a common
csolution: define achararray in place of a bit vector. Suppose you need 32 bits which equates to 4 bytes. Create a char array of size 4 (char my_bits[4]). This will allocate a contiguous section of memory with 32 bits as shown below.
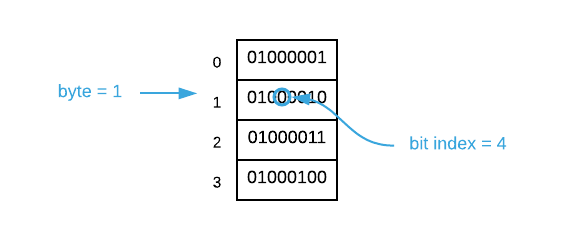
To address individual bits, you must first find the byte in which the target bit resides. Assuming the index is represented by $i$, this is calculable using the following formula $\left \lfloor \frac{i}{8} \right \rfloor$. Next, you find the index of the bit inside the byte using the formula $i \bmod 8$. Finally, you can set the bit using a bitwise operation as follows:
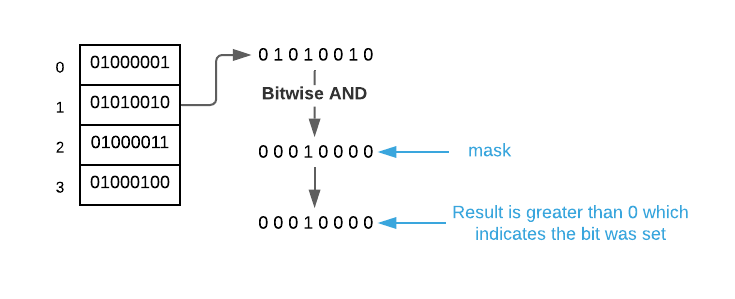
my_bits[byte_index] = my_bits[byte_index] | 1 << bit_index. A different bitwise operation is used to retrieve the value of a bit:my_bits[byte_index] & 1 << bit_index.Continuing on with the example, assume you need to set the value of bit $\blueci{12}$. The byte index is $\left \lfloor \frac{\blueci{12}}{8} \right \rfloor = 1$ and the bit index is $\blueci{12} \bmod 8 = 4$. Consult the image below.
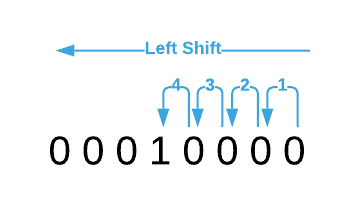
To set the bit, you must first create a mask which is simply a byte with all values except the bit in question set to
0. In this case, the command1 << 4creates the mask. It results in the bit pattern00010000; that is, the value of00000001left shifted 4 bits. See the image below.
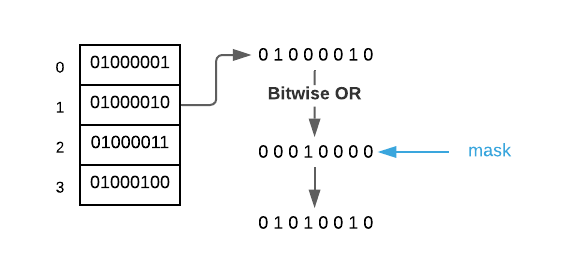
The final step is to bitwise
or(|) the two values together as shown below.
Determining the value of a bit is similar. The only difference is that the target byte is
and‘ed (&) with the mask. If the resulting value is greater than zero, the bit was set.
This was a quick review of the bitwise operations required to create a bloom filter. Readers are encouraged to do further research in the event that these concepts are foreign to them.
Source Code
Relevant Files:
Click here for build and run instructions
Exercises
-
Answer true of false to each of the following:
a. A bloom filter may return adoes not existresponse for an item that was previously inserted.
b. A bloom filter may return anexistsresponse for an item that was NOT previously inserted.
c. It is possible to implement a bloom filter in such a way that the error rate is 0%.
d. It is possible for a bloom filter to resize itself when it becomes too full.Answers (click to expand)
- False - An insert operation sets all associated bits to `1`. No subsequent operations have any possibility of setting any bit value to `0`.
- True - It is possible that insert operations based on other keys set all of the bits to `1` for the key in question.
- False - Regardless of the number of hash functions and the size of the bit vector, there is always a possibility false positive results.
- False - Each computed hash is compressed into a bit vector index. An input to the compression function is the bit vector size. Changing the size requires recalculating all of the hashes. The bloom filter does not have access to the originally inserted keys so this is not possible.
-
For each of the following, specify which bloom filter implementation detail(s) results in:
a. lower memory consumption
b. faster performance
c. lower error rateAnswers (click to expand)
- Each hash function and bit consumes memory; therefore, reducing either will shrink the footprint.
- Each hash function must be computed separately; therefore, reducing the number of functions will reduce the overall computational load.
- As demonstrated in the provided equations, increasing the size of the bit vector and number of functions trends asymptotically toward a 0% error rate.
-
What is most important dimension of a space-efficient probabilistic data structure: error rate, memory consumption, or performance?
Answers (click to expand)
None of the above. It nonsensical to evaluate trade-offs outside of a specific application context. A cloud-based application serving thousands of requests per second may need to prioritize performance. A memory constrained embedded application may need to optimize its footprint. The criticality of the result determines the tolerable error rate.
-
Assume that you are charged with implementing a bloom filter expected to hold 1,500 keys. Specify the error rate, bit vector size, and number of hash functions given the following constraints:
a. There are 10 available hash functions and the maximum bit vector size is 480 bits.
b. An error rate of $\approx .04$.
c. An error rate of $\approx .01$Answers (click to expand)
- The number of hash functions and bit vector size are pre specified. The only thing left to do is plug the value into the equation to get the error rate. $$ P=(1-[1-\frac{1}{m}]^{^{kn}})^k\\ n = 1500, m = 480, k = 10\\ P=(1-[1-\frac{1}{480}]^{^{10 \times 1500}})^{10}=.\overline{9}\\ $$ Obviously, these parameters aren't desirable. There is close to a 100% probability of error.
- The error rate is pre specified, so the other two variables must be derived from the equations. First, calculate the number of required bits. $$ m=-\frac{n\ln P}{(\ln2)^2}\\ m=-\frac{1500\ln .04}{(\ln2)^2} \approx 10049.5 $$ The total number of bits is rounded up to $10050$. Due to memory being available in 8 byte chunks, that rounds up to $10056$ bits or $1257$ bytes. The only thing left to do is calculate the number of hash functions. $$ k=\frac{m}{n}\ln 2\\ k=\frac{10056}{1500}\ln 2 \approx 4.6 $$ To achieve an error rate of $\approx .04$ with $1500$ items, a bit vector of $1257$ bytes and 5 hash functions are required.
- The error rate is pre specified, so the other two variables must be derived from the equations. First, calculate the number of required bits. $$ m=-\frac{n\ln P}{(\ln2)^2}\\ m=-\frac{1500\ln .01}{(\ln2)^2} \approx 14377.6 $$ The total number of bits is rounded up to $14378$. Due to memory being available in 8 byte chunks, that rounds up to $14384$ bits or $1798$ bytes. The only thing left to do is calculate the number of hash functions. $$ k=\frac{m}{n}\ln 2\\ k=\frac{14384}{1500}\ln 2 \approx 6.6 $$ To achieve an error rate of $\approx .01$ with $1500$ items, a bit vector of $1798$ bytes and 7 hash functions are required.
-
Using the programming language of your choice, create a general purpose bloom filter. Consumers of your data structure must have the ability to adjust the error rate, memory consumption, and performance to suit their needs.
Answers (click to expand)
See the C implementation provided in the links below. Your implementation may vary significantly and still be correct.
- bloom_filter.h
- bloom_filter.c
- bloom_filter_test.c
-
To be precise, they determine set membership with a probability of false positive results. This will be covered in more detail later. ↩
-
The numbers provided in this image are for demonstration purposes only. It’s possible to get the same result using 32 or 128-bit hashes. Additionally, the total bloom filter size is dependent on many implementation details. ↩
-
As Arthur C. Clarke said, “any sufficiently advanced technology is indistinguishable from magic”. ↩
-
A bit vector is nothing more than an array of bit (
0or1) values. Imagine an area of memory where each bit can be modified like an array element. A typical array is not suitable because they store at least a single byte per array element which is wasteful in this context. ↩ -
Review hashing and hash compression for more details on converting an input value to an array index. ↩
-
Obviously, no list of computer scientist would be complete without them! ↩
-
Here is a good place for those curious about bloom filter math to start ↩
-
For example, https://hur.st/bloomfilter/ ↩
-
For instance, some systems forbid the most commonly used and therefore easily breakable passwords. https://www.atechjourney.com/most-common-passwords/ ↩