Finding the Maximum Weighted Independent Set for graph is an $NP$-hard problem. Therefore, this section focuses on finding the Maximum Weight Independent Set for the specific case of Path Graphs. Although not explicitly demonstrated here, the algorithm is expandable to tree graphs with some minor alterations. First, we review the salient graph concepts including Independent Sets and Path Graphs.
Conceptually, an Independent Set (IS) is comparable to the inverse of a graph. It’s a set of vertices that do not contain both endpoints of any edge. Consider a connected graph with only three vertices as shown below. There are five independent sets.
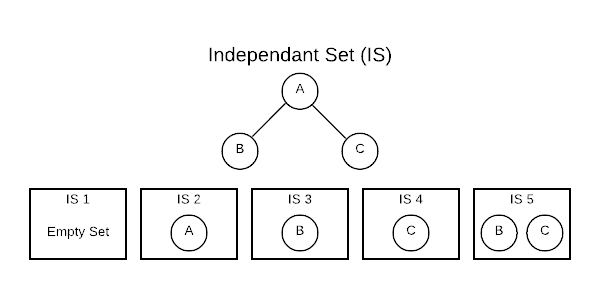
The [] (empty set) is always considered an IS because it technically fits the
definition. The sets [A], [B], and [C] are also ISs because no edge
contains only one vertex. The set [B, C] also qualifies because there are no
edges connecting B and C. One important thing to note is that the number of
ISs grows exponentially as the number of vertices grow. This has important
algorithmic implications.
At first glance, this concept seems a bit academic; however, ISs are useful in practice. Finding an IS is a way of asking, which vertices do not have a relationship. For instance, if vertices are people and edges are familial relationship, an IS would define people who are not related.
A path graph has vertices that can be listed in order $v_1, v_2, …,v_n$ such that edges are ${v_i, v_{i+i}}$ where $i = 1, 2, …, n-1$. That is rather complicated definition for a simple concept that is easily visualized. The image below represents a path graph.

There is only one path through the graph and each vertex is connected to the preceding vertex. By this definition, there will always be $n-1$ edges.
With preliminary concepts out of the way, it’s time to define the problem that this algorithm is designed to solve. Given a path graph where each vertex has an associated non-negative weight, find the independent set with the highest cumulative weight.
Applications
- Set packing
Asymptotic Complexity
\(O(n)\)
Pseudo Code
The pseudo code below is a particularly slow implementation ($O(n^2)$) of a maximum independent set algorithm. However, it will help the reader understand the mechanics before examining the more complex version below.
max_weight_is:
inputs:
V = array of vertices arranged to represent a path graph
n = number of vertices
if n = 0:
return [] // Empty Set
if n = 1:
return V
result1 = max_weight_is V[0] - V[n - 1] // recurse
result2 = max_weight_is V[0] - V[n - 2] // recurse
if(result1 > result2 + V[n])
return result 1
else
return result2 + V[n]
The version below has an optimal run time ($O(n)$).
max_weight_is:
inputs:
V = array of vertices arranged to represent a path graph
n = number of vertices
S = solutions array of size n + 1
S[0] = []
S[1] = V[0]
i = 2 to n:
if S[i-1] > S[i-2] + V[i-1]:
S[i] = S[i-1]
else
S[i] = S[i-2] + V[i-1]
return S[n+1]
Source Code
Relevant Files:
Click here for build and run instructions