Union-Find (Disjoint Set)

graph LR
	ALG(["fas:fa-trophy Union Find fas:fa-trophy #160;"])

	ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
    click ASY_ANA "./math-asymptotic-analysis"

	SN(["fas:fa-check Set Notation #160;"])
    click SN "./math-set-notation"

	ASY_ANA-->ALG
    SN-->ALG

The Union-Find, aka Disjoint-Set, data structure¹ is a deceptively simple algorithm for identifying the disjoint sets in a collection. That is, sets that have no common elements. Stated more rigorously, sets $A$ and $B$ are disjoint if $A \cup B = \emptyset$. It can be difficult to visualize because it’s an inherently abstract concept.

History

The notion of disjoint sets has been in use by mathematicians since the late 1800s. The union-find algorithm was first introduced in 1964 in a paper entitled An Improved Equivalence Algorithm by Bernard A. Galler and Michael J. Fischer². What’s particularly interesting about this data structure is how it shaped the analysis of algorithms.

At the time of first publication, the practice was not sufficiently evolved enough to accurately specify the algorithm’s asymptotic complexity. In 1973, J. E. Hopcroft and J. D. Ullman published a proof³ that bounded the algorithm at $O(\log^*{n})$⁴. Robert Tarjan published a stronger proof⁵ in 1975 that specified an even lower bound of $O(m \alpha(n))$ where $\alpha$ is the inverse Ackerman function⁶. While it’s true that difference in time bounds is negligible at best, the proofs are excellent examples of algorithmic analysis techniques.

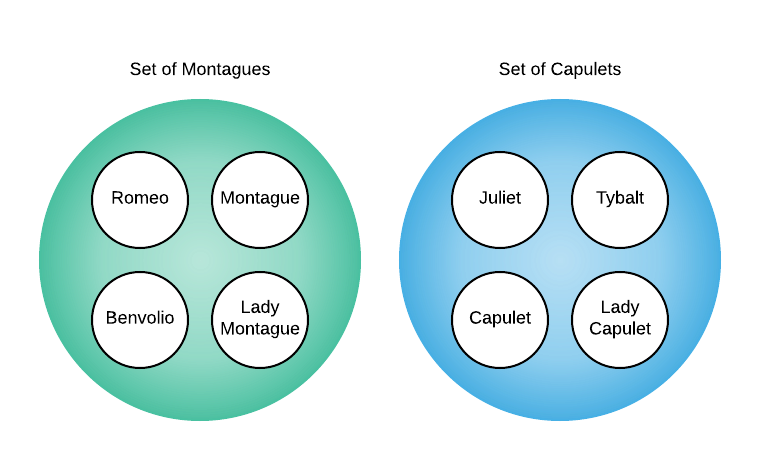
To elucidate, consider popular characters from Romeo and Juliet: Romeo, Juliet, Tybalt, Capulet, Lady Capulet, Montague, Lady Montague, and Benvolio⁷. For the purposes of this example, a set is defined by family relations. At the beginning of the play, the characters form two distinct disjoint sets as shown below.

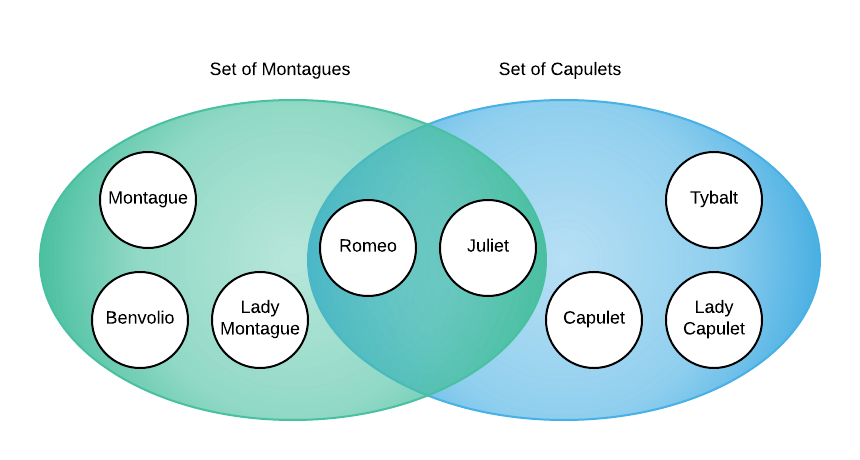
Act 2, scene 5 changes the makeup of the sets when Juliet and Romeo marry. The Montague and Capulet sets are no longer disjoint because they share elements as the image below illustrates.

Consider how one might write an algorithm to divine if there are disjoint sets among an evolving set of random objects. Conceptually, the union-find data structure accomplishes this by first defining each object as an independent set and allowing consumers to merge individual items. Merging any two items results in merging their sets. If merging all items results in a single set, there are no disjoint sets. This is shown graphically below.

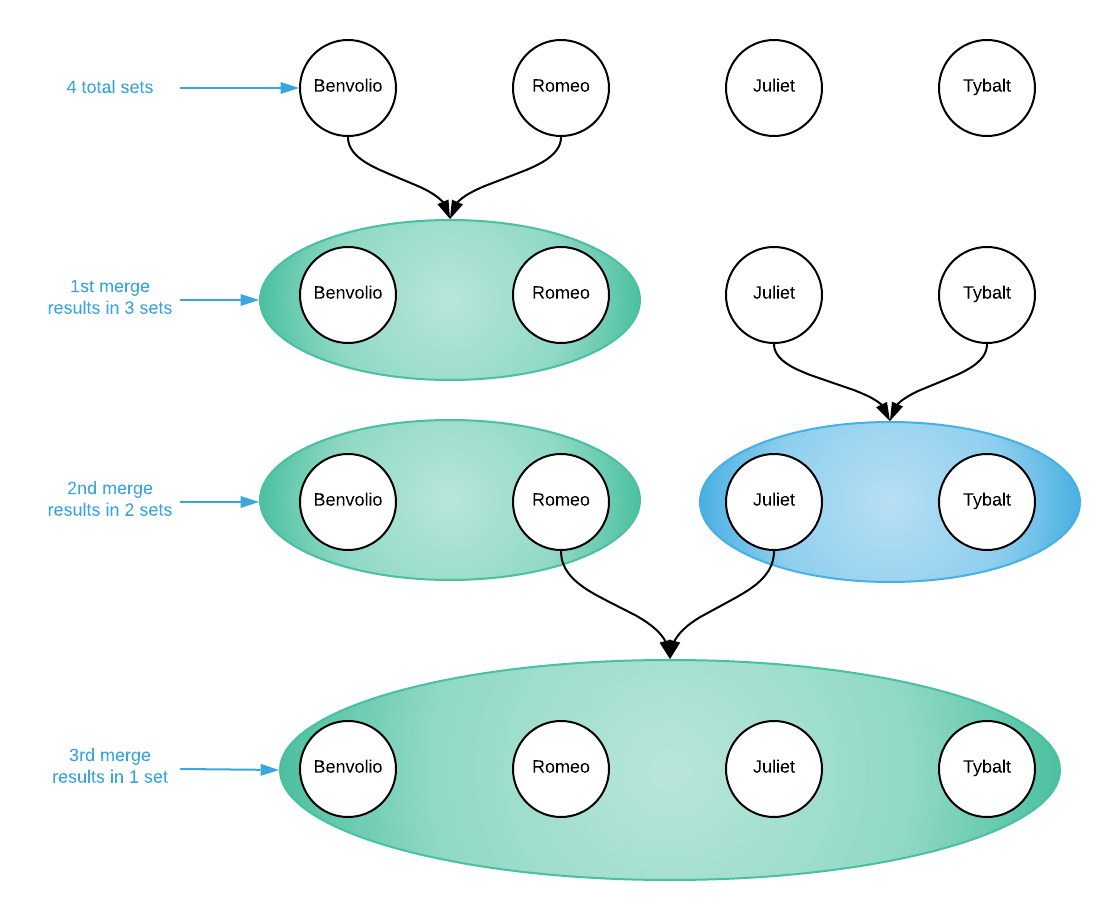
This sub-section outlined the conceptual operation of the union-find data structure, the next describes how this is accomplished.

Union Find Interface

The union-find data structure’s abstract interface defines three operations: make set, union, and find. make set creates a new set. Sets are tree data structures. Each set has a set representative that resides at the root of the tree and each object maintains a pointer to its parent. The representative’s parent pointer is self-referential. Starting at any object, following parent pointers will always lead to the set representative. union merges the sets of two items into one and find returns the set representative for which the item belongs. This is best demonstrated graphically.

The picture below is a representation of a union-find data structure after 6 make set operations (make set A; make set B; ...). Notice how each object created a distinct set with a single member that has a self-referential pointer. At this point, every object is a set representative.

Executing a union operation on A and C deletes set-3 and merges C into set-1. A is still the set representative but now C’s parent pointer points to A.

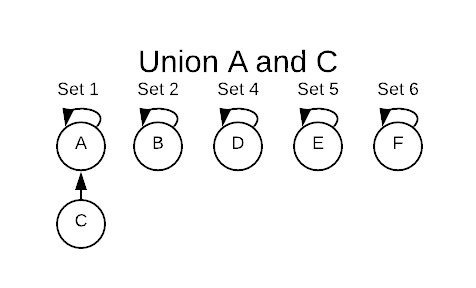
Executing a union operation on A and D deletes set-4 and merges D into set-1.

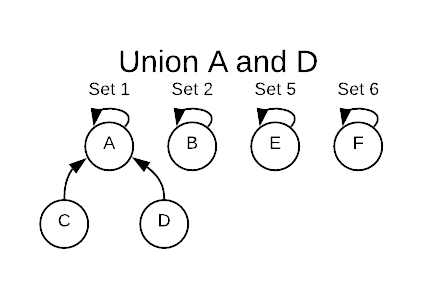
Executing a union operation on E and F deletes set-6 and merges F into set-5.

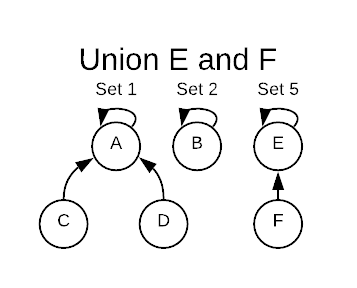
Finally, executing a union operation on E and A merges set-5 into set-1 leaving only two remaining sets.

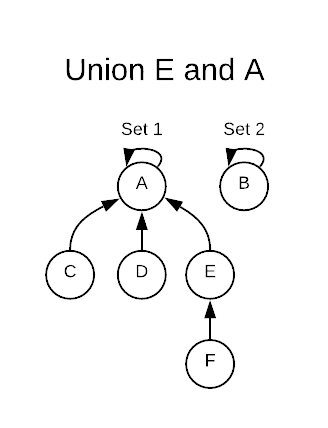
The find operation returns the set representative for which an object is contained. Consider the image above. find F will return Set-1’s representative A. Staring at F, it follows the pointers until it reaches A which has a self-referential loop. This indicates that it has found its containing set.

Improving Performance

There are two techniques that significantly improve the performance of union-find data structures: union by rank and path compression.

Union by rank ensures that when two sets are merged, each leaf of the tree will have the shortest possible path to the root. Shorter paths mean fewer traversals for each find operation. Consult the image below. There are two possibilities for merging set-1 and set-2. If set-2 is consumed by set-1, it results in more work for the find operation.

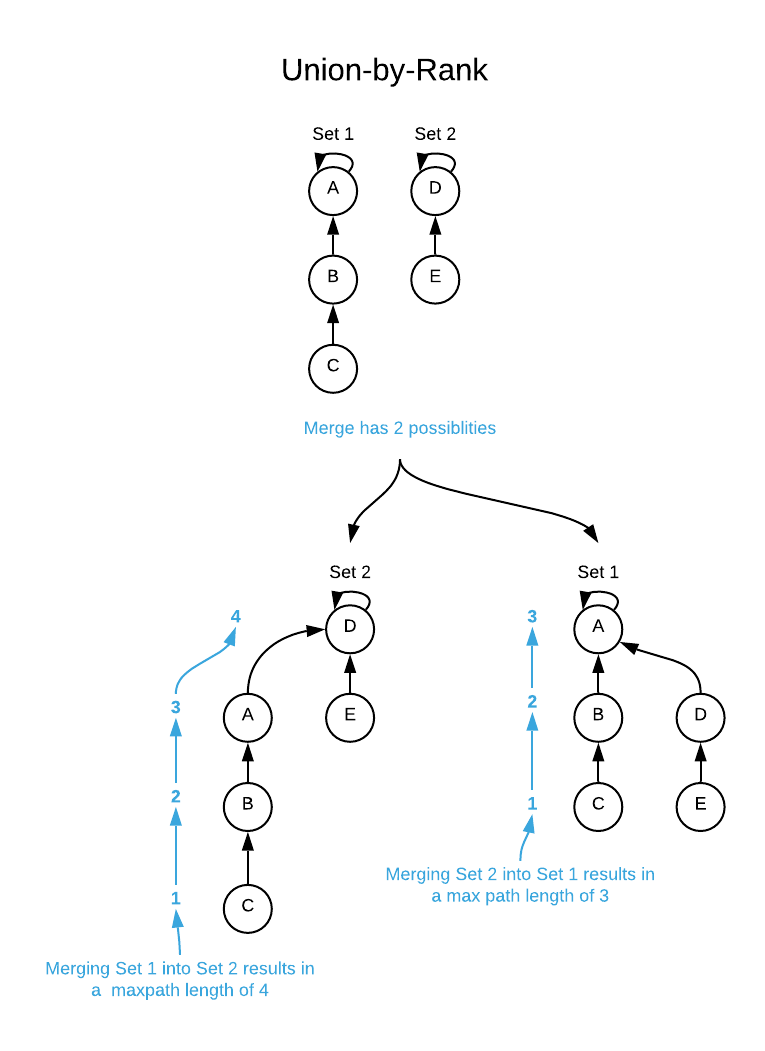
The general idea is to maintain a rank value for each set. Lower ranks are always consumed into sets with higher ranks. See the pseudo code for more details.

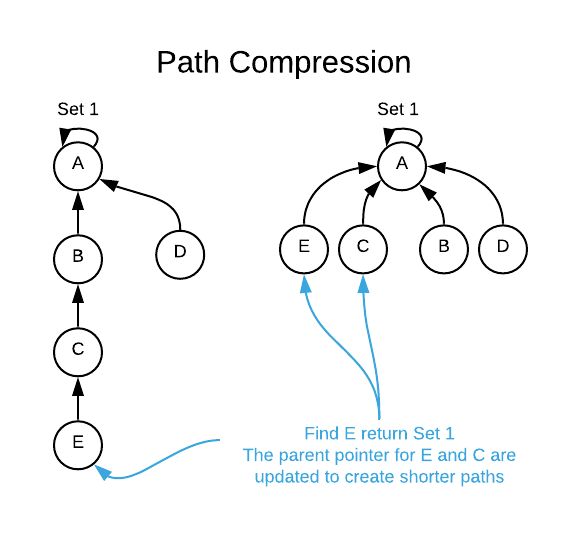
Path compression takes advantage of the find operation. Each find operation requires a path traversal to the root. It takes no extra time to update each node to point directly to the root thereby compressing the path. This is depicted graphically below.

In conclusion, the union-find data structure is deceptively simple yet is sometimes difficult to comprehend due to its abstract nature. It’s purpose is to identify disjoint sets within a collection of loosely connected objects.

Applications

• Kruskal’s Minimum Spanning Tree
• Detecting cycles in a graph

Asymptotic Complexity

• Make Set: $\Theta(1)$
• Union: $O(n), \Omega(1)$
• Find: $O(n), \Omega(1)$

The bullet points above, though accurate in the most technical sense, are deceiving. While it’s true that a single union or find operation may take $O(n)$, it’s actually closer to $\Theta(1)$. Remember that each find operation reduces the run time to $\Theta(1)$ for all future find operations for all nodes in the path.

Assume that $n$ is the number of make set operations and $m$ is the total number of make set, union, and find operations combined⁸. The amortized asymptotic complexity works out to $O(m \alpha(n))$ Where $\alpha$ is the inverse Ackerman function. The particulars of the function are not important. The salient concept is that the function grows very slowly. It will not exceed $4$ for values of $n$ as high as $10^{600}$. For all practical intents and purposes, one can assume all operations are constant ($\Theta(1)$).

Pseudo Code

\begin{algorithm}
\caption{Union Find Data Structure}
\begin{algorithmic}
\REQUIRE obj = obj that will act as a set representative
\ENSURE obj becomes a set representative
\FUNCTION{makeset}{obj}
    \STATE obj.parent $\gets$ obj
    \STATE obj.rank $\gets$ 0
\ENDFUNCTION
\STATE
\REQUIRE obj = obj to find representative for
\OUTPUT obj that is the representative obj's set
\FUNCTION{find}{obj}
    \IF{obj.parent != obj}
        \STATE obj.parent $\gets$ \CALL{find}{obj} \COMMENT{path compression}
    \ENDIF
    \RETURN{obj.parent}
\ENDFUNCTION
\STATE
\REQUIRE x = an initialized with the makeset method
\REQUIRE y = an initialized with the makeset method
\ENSURE the sets represented by x and y are merged into a single set
\FUNCTION{union}{x, y}
    \STATE set1 $\gets$ \CALL{find}{x}
    \STATE set2 $\gets$ \CALL{find}{y}
    \IF{set1 = set2}
        \RETURN{}
    \ENDIF
    \STATE
    \IF{set1.rank $\gt$ set2.rank} \COMMENT{union by rank}
        \STATE set2.parent $\gets$ set1
    \ELSE
        \STATE set1.parent $\gets$ set2
        \IF{set1.rank = set2.rank}
            \STATE set2.rank $\gets$ set2.rank + 1
        \ENDIF
    \ENDIF
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}

Implementation Details

For the sake of brevity, this pseudo code makes two assumptions: the first is that it does not need to maintain the total number of sets and the second is that it can freely modify objects (see lines 3 and 4). This will NOT be the case for general-purpose union-find data structures.

A common implementation technique is to maintain a hash table of sets using the objects themselves as keys. The code below is a simplified representation of the approach.

// error handling is omitted for brevity
void make_set(DisjointSet* self, void* obj) {
    Set* new_set = malloc(sizeof(Set));
    new_set.rank = 0;
    new_set.parent = new_set;
    // self.sets is a hash table, obj is the key value, and new_set is the stored object
    HashTable_Put(self.sets, obj, new_set);
}

void find(DisjointSet* self, void* obj) {
    // self.sets is a hash table, obj is the key value
    Set* set = HashTable_Get(self.sets, obj);

    if (set.parent != set)
        return find(set.parent);

    return set.parent;
}

Source Code

Full Repo

Relevant Files:

• disjoint_set.h
• disjoint_set.c
• disjoint_set_test.c

Click here for build and run instructions

Exercises

1. Assuming you have invoked $n$ make set operations on a union-find data structure:
   a. What is the maximum number of union operations that can be invoked on items contained in disjoint sets?
   b. Does the answer to question a change depending on the order in which constituent items are merged?

   Answers (click to expand)

   1. $n-1$ - Every successful union operation results in reducing the total number of sets by 1.
   2. No, items can be merged in any order and achieve the same results.

2. Assume you have an empty union-find data structure, define the resulting sets given the following sequence of operations:
   a. make_set(A), make_set(B), make_set(C), union(A,C), union(B,C)
   b. make_set(A), make_set(B), make_set(C), make_set(D), union(A,D), union(B,C), union(C,D)
   c. make_set(A), make_set(B), make_set(C), union(A,B), make_set(D), union(B,C), union(A,C)

   Answers (click to expand)

   a.

   make_set(A) = {A}
   make_set(B) = {A}, {B}
   make_set(C) = {A}, {B}, {C}
   union(A,C) = {A, C}, {B}
   union(B,C) = {A, C, B}
   

   b.

   make_set(A) = {A}
   make_set(B) = {A}, {B}
   make_set(C) = {A}, {B}, {C}
   make_set(D) = {A}, {B}, {C}, {D}
   union(A,D) = {A, D}, {B}, {C}
   union(B,C) = {A, D}, {B, C}
   union(C,D) = {A, D, B, C}
   

   c.

   make_set(A) = {A}
   make_set(B) = {A}, {B}
   make_set(C) = {A}, {B}, {C}
   union(A,B) = {A, B}, {C}
   make_set(D) = {A, B}, {C}, {D}
   union(B,C) = {A, B, C}, {D}
   union(A,C) = {A, B, C}, {D} // no change, the two sets are already merged
   

3. The romeo_juliet_graph.txt text files describes the relationships of Romeo and Juliet characters. Each line represents such a relation in the following format:
   {Character}<tab>{Relationship}<tab>{Character}
   Possible relationships include knows and kin. Using the programming language of your choice, write a program that:

   • parses the file
   • creates a set in a union-find data structure for each distinct character
   • unions each set of characters that have a kin relationship
   • displays the resulting sets
   Answers (click to expand)

   See the C implementation provided in the link below. Your implementation may vary significantly and still be correct.
   disjoint_set_test_case.c
   The final output should resemble:

   total number of sets = 9
   Set Representative = Friar Laurence, Members = Friar Laurence
   Set Representative = Benvolio, Members = Benvolio
   Set Representative = Apothecary, Members = Apothecary
   Set Representative = Friar John, Members = Friar John
   Set Representative = Mercuito, Members = Mercuito
   Set Representative = Nurse, Members = Nurse
   Set Representative = Romeo, Members = Lord Montague, Romeo, Lady Montague
   Set Representative = Prince, Members = Prince, Paris
   Set Representative = Juliet, Members = Juliet, Tybalt, Lady Capulet, Lord Capulet