Under Construction: Consider this content a preview of the real thing which is coming soon (hopefully).
graph LR
classDef currentPage stroke:#333,stroke-width:4px
ALG(["fas:fa-trophy Algorithmis fas:fa-trophy "])
ASY_ANA(["fas:fa-check Asymptotic Analysis#160;"])
click ASY_ANA "./math-asymptotic-analysis"
MAT_NOT(["fas:fa-check Mathematical Notation#160;"])
click MAT_NOT "./math-notation"
POL(["fas:fa-check Polynomials #160;"])
click POL "./math-polynomials"
MAT_FUN(["fas:fa-check Math Functions#160;"])
click MAT_FUN "./math-functions"
LOG(["fas:fa-check Logarithms#160;"])
click LOG "./math-logarithms"
COM(["fas:fa-check Combinatorics#160;"])
click COM "./math-combinatorics"
SET_NOT(["fas:fa-check Set Notation#160;"])
click SET_NOT "./math-set-notation"
GRA(["fas:fa-check Graphing#160;"])
click GRA "./math-graphing"
class GRA currentPage
BW(["fas:fa-check Bitwise Logic#160;"])
click BW "./math-bitwise"
MAT(["fas:fa-check Matrices#160;"])
click MAT "./math-matrices"
ASY_ANA-->ALG
BW-->ALG
MAT-->ALG
COM & GRA & SET_NOT-->ASY_ANA
MAT_NOT--> SET_NOT
POL & LOG--> MAT_FUN
MAT_FUN--> GRA
A function is representable as a curve in space where the vertical direction symbolizes the output and the horizontal direction symbolizes the input. The connection between polynomials as geometric objects and their algebraic properties is profound.
\[x^3 - x - 1\]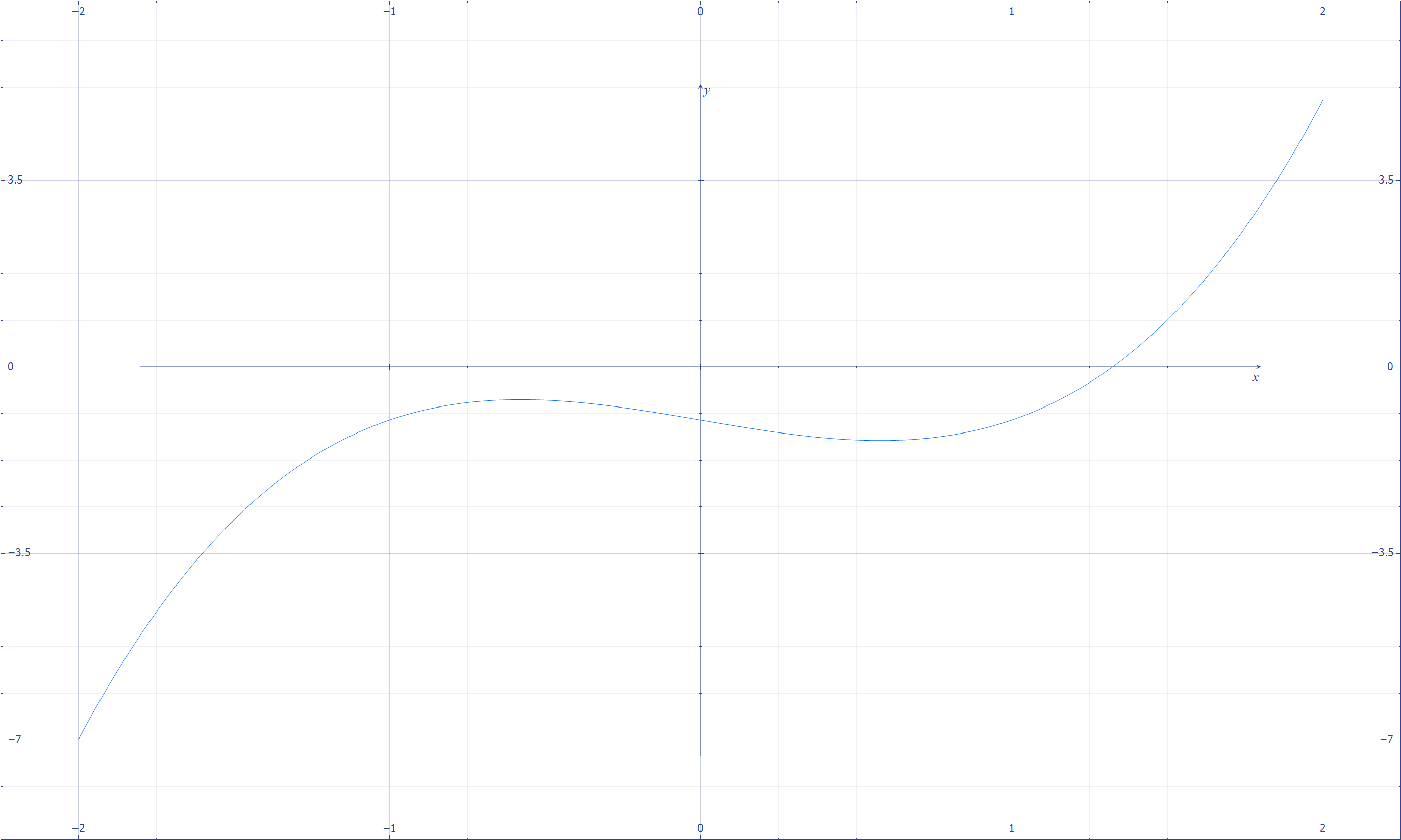
Descartes graphical representation of polynomials