Prerequisites (click to view)
graph LR
ALG(["fas:fa-trophy Linked List fas:fa-trophy #160;"])
ASY_ANA(["fas:fa-check Asymptotic Analysis #160;"])
click ASY_ANA "./math-asymptotic-analysis"
SARRAY(["fas:fa-check Sorted Array #160;"])
click SARRAY "./list-data-struct-sorted-array"
ARRAY(["fas:fa-check Array #160;"])
click ARRAY "./list-data-struct-array"
SARRAY-->ALG
ARRAY-->ALG
ASY_ANA-->ALG
The linked list is a simple yet powerful data structure. Much like an array, a linked list tracks a collection of arbitrary elements. However, unlike an array, items are not required to be stored contiguously, individual elements can be disparately sized, and insert\delete operations are constant time1. The trade off for this added utility is that it is not possible to divine the address of constituent items in constant time which makes efficient sorting and searching problematic.
History
Linked lists were incepted by Allen Newell, Cliff Shaw, and Herbert A. Simone of the RAND Corporation in 1955 as the primary data structure for IPL (Information Processing Language). Many later languages drew inspiration from IPL and “baked” them in as a core language construct. One of the most notable examples is LISP which was created by John McCarthy in 1958. LISP is the archetype language for the functional programming paradigm.
Each element in a linked list contains a pointer (see the Pointer sub-section below for a quick primer) to its sibling. The image below illustrates how a linked list containing four integer values might be laid out in memory2.
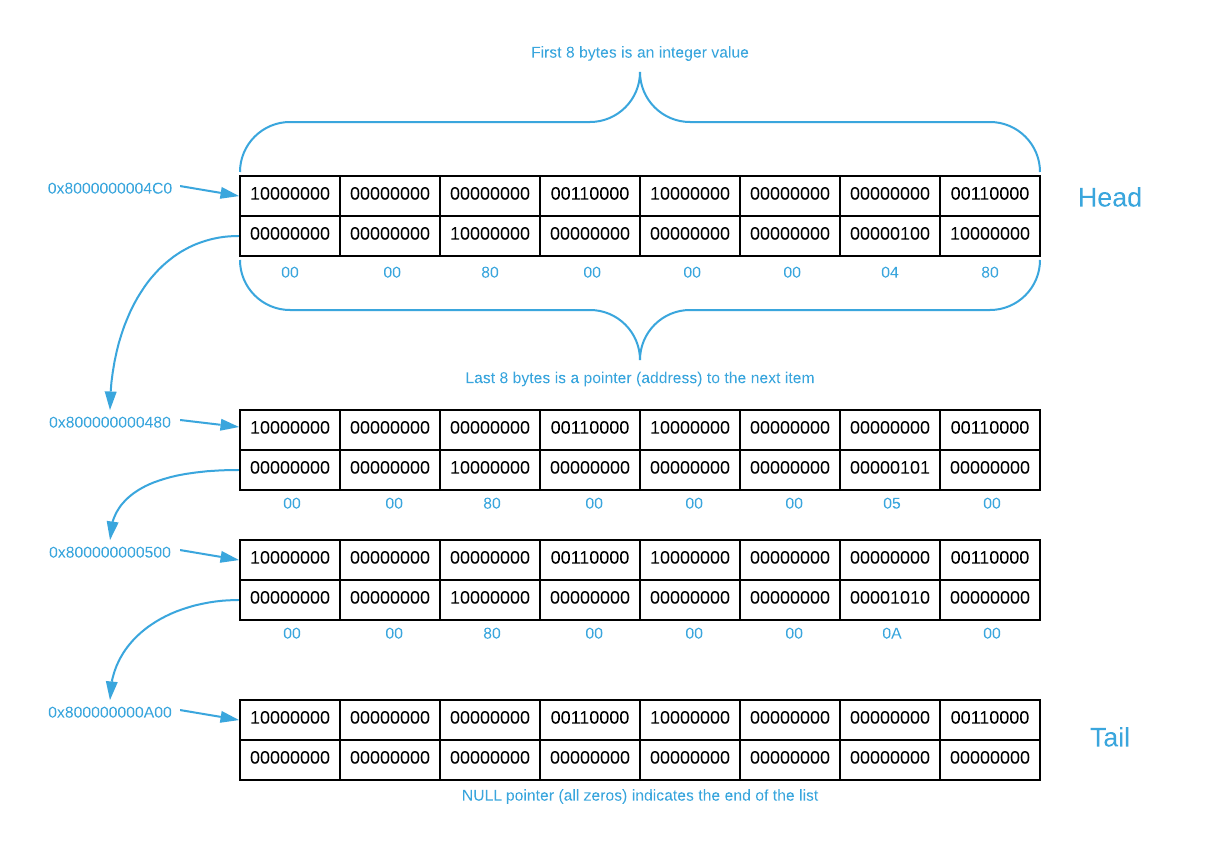
There are a few things to note. By convention, the first item in a linked list
is known as the head and the last item is known as the tail. The tail’s
pointer value is NULL. List traversal involves starting at the head and
continuously following pointers until a NULL value is encountered. Notice that
the starting address of each constituent item is arbitrary. Because of this,
it’s easy to insert elements by simply changing pointer values as illustrated
below. The same is true for deleting items.

The trade off is that that the only way to locate items in the list is via link traversal3. Unlike arrays, there is no formula for divining the memory location of the individual elements. For instance, if you are interested in item number two, you must first access the head, follow its link to item number one, and likewise follow its link to item two. An epiphenomenon is that efficient search algorithms such as binary search (see Sorted Array) aren’t possible because there is no way to quickly locate the middle of the list.
A final consideration is that it is possible to create a linked list with poor spatial locality; that is, the location of items can be distributed in such a way as to confound a machine’s ability to efficiently use the memory cache hierarchy. Depending on the machine architecture, temporal access pattern, and the size of individual elements, this could lead to significant performance degradation.
Types of Linked Lists
There are several varieties of linked lists; the three most common of which are illustrated below.

Singly linked lists (as depicted in the opening section) can only be traversed in a single direction. A slight variation is the circular linked list which simply points the tail back to the head. Finally, a doubly linked list includes a pointer to the next item as well as the previous. This provides dual direction traversal with the trade offs of memory overhead and complexity.
Pointers
Although not specifically a linked list topic, pointers fuel the fitful
nightmares of many young programmers; therefore, it’s worth a quick primer. The
way a machine interprets data stored in memory is contingent on two factors: the
state (zero or one) of the bits and the instruction context. Stated differently,
a bit pattern in and of itself has no inherit meaning. The instructions acting
upon an arrangement of bits provide the interpretive context required to derive
meaning. As an example, consider the eight bytes: 10000100 01000001 00110111
01110000 00100001 00100011 01100110 01100111. The table below outlines a few
possible machine interpretations.
| Data Type | Value |
|---|---|
| 8 8-bit ASCII Characters | A7p!#fg |
| 64-bit Unsigned Integer | 9529959241224513127 |
| 64-bit Signed Integer4 | -8916784832485038489 |
| 64-bit Floating Point5 | $\approx$-3.533299 |
| 64-bit Address | 0x8441377021236667 |
Notice the last entry in the table: 64-bit address6. An address is nothing more than a number that points to a specific byte location, hence the name pointer. The pointer tells the machine, act on the bit pattern starting at this address. Pointers have no way of specifying the actual number of bytes they point to. The instruction context tracks these details. In the case of linked lists, pointers specify the starting address of sibling items. The instruction context determines how to interrupt the data stored at the address.
In the simplest terms, a pointer is just a section of memory that holds the address of another section of memory. No more nightmares.
Applications
- Countless general purpose programming tasks
- Building block for several more complex data structures including stack, queue, binary tree and hash table to name a few.
- The
Cstandard library uses linked lists to track heap allocations (mallocandfree) -
The previous and next navigation buttons employed by most browsers. See the Chrome screenshot below.
Pseudo Code
\begin{algorithm}
\caption{Linked Lists}
\begin{algorithmic}
\REQUIRE item = item to insert
\REQUIRE predecessor = linked list item that should precede item
\FUNCTION{insert}{item, predecessor}
\STATE $\text{item}_{next} \gets \text{predecessor}_{\text{next}}$
\STATE $\text{predecessor}_{\text{next}} \gets$ address of item
\ENDFUNCTION
\STATE
\REQUIRE item = item to delete
\REQUIRE predecessor = linked list item precessing item
\FUNCTION{delete}{item, predecessor}
\STATE $\text{predecessor}_{\text{next}} \gets \text{item}_{next}$
\ENDFUNCTION
\STATE
\REQUIRE item linked list head
\REQUIRE value = value to search for
\OUTPUT item with value = value if it exists, otherwise $\text{NOT_FOUND}$
\FUNCTION{search}{item, value}
\STATE current $\gets$ item
\WHILE{current $\neq$ NULL}
\IF{$\text{current}_{\text{value}}$ = value}
\RETURN current
\ENDIF
\ENDWHILE
\RETURN $\text{NOT_FOUND}$
\ENDFUNCTION
\STATE
\REQUIRE item = linked list head
\REQUIRE func = function to apply to each item
\FUNCTION{enumerate}{item, func}
\WHILE{item $\neq$ NULL}
\STATE \CALL{func}{item}
\STATE item $\gets \text{item}_{next}$
\ENDWHILE
\ENDFUNCTION
\end{algorithmic}
\end{algorithm}
Asymptotic Complexity
- Insert: $O(1)$
- Delete: $O(1)$
- Search: $O(n)$
- Enumerate: $\Theta(n)$
Advantages
- Insert/Delete: Constant time operation
- Maintains Insertion Order: Maintains the order in which items are inserted.
Disadvantages
- Memory: Each individual element must maintain one or more additional pointers.
- Spatial Locality: It’s possible to distribute items throughout memory in a non-optimal way.
- Search: There is no inherit support for search operations other than examining each item individually. Linked lists cannot take advantage of algorithms such as binary search, regardless of the sort order.
Source Code
Relevant Files:
Click here for build and run instructions
Exercises
-
Assuming a 64-bit architecture, what is the amount of memory required to store:
a. 16 64-bit integers in an Array
b. 16 64-bit integers in a Singly linked list
c. 16 64-bit integers in a Doubly linked list
d. 16 64-bit pointers to 128 bit strings in an ArrayAnswers (click to expand)
- Arrays have no memory overhead. A 64-bit number occupies 8 bytes. If there are 16 numbers, the answer is $8\text{ bytes} \times 16 = 128\text{ bytes}$.
- Each list element contains a 64-bit integer and a 64-bit pointer. That works out to 16 bytes per item. There are 16 items. The total amount of memory is $16 \text{ bytes} \times 16 = 256 \text{ bytes}$.
- Each list element contains a 64-bit integer and two 64-bit pointers. That works out to 24 bytes per item. There are 16 items. The total amount of memory is $24 \text{ bytes} \times 16 = 384 \text{ bytes}$.
- The array itself contains 16 8-byte pointers for a total of $8\text{ bytes} \times 16 = 128\text{ bytes}$. Recall that a pointer is just an address. The size of the data that's it's pointing to is irrelevant to the question.
-
Assuming you do not know the address of the 3rd item, how would you go about inserting an item in the 4th position of a singly linked list.
Answers (click to expand)
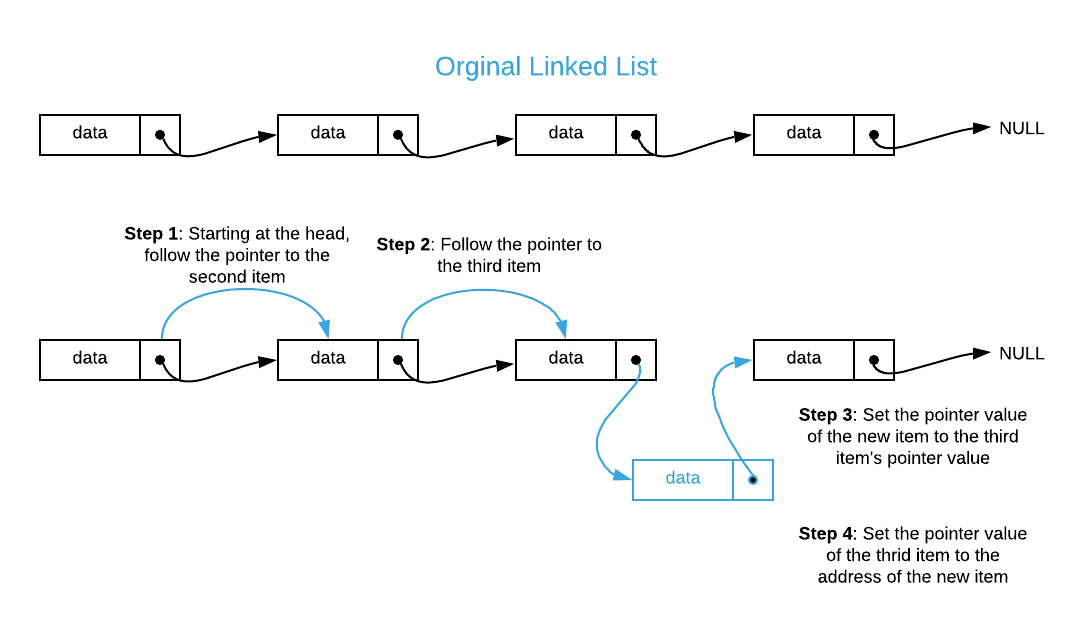
-
Using the supplied answer to question 2, is it possible to swap the order of steps 3 the 4?
Answers (click to expand)
No, if you overwrite the predecessor's next pointer, you will not know what value to set the new item's next pointer to.
-
Assuming the data is pre-sorted, is it possible to adapt the binary search algorithm to work with a doubly linked list in $O(\log_2{n})$ time?
Answers (click to expand)
No, it is not possible. See line 6 of the binary search algorithm. It requires the ability to jump to the middle of a list. This isn’t possible with any linked list.
-
Define the pseudo code for the following operations on a doubly linked list.
a. Given an existing item and a new item, insert the a new item directly after the existing item
b. Delete an item
c. Given a list head, new item, and index, insert the new item at the ordinal index positionFor formatting purposes, the answers for question 5 are located here.
-
This assumes that you know the address of the item you want to delete. In the case of an insert, you need to know the address of the item that you want to insert adjacent to. ↩
-
Although most processor architectures (x86 and ARM) use little-endian; the bytes are shown in big-endian byte order to aid readability. ↩
-
Assuming you do not know the address of the item. ↩
-
Assuming two complement, which is the most common way to store signed integers. ↩
-
Assuming the IEEE-754 floating-point standard ↩
-
The size of an address is dependent on the machine architecture. A 32-bit machine address is four bytes long, a 64-bit machine address is eight bytes long. Most modern machine architectures are 64-bit. However, some modern low power devices have 32-bit architectures. There are also many older 16 and 24 bit architectures still in use today as well as a plethora of esoteric machines with different address spaces. ↩