A graph with no cycles is said to be acyclic. A directed acyclic graph is particularly interesting because such graphs have a least one (usually many) topological ordering. A graph with a cycle has no topological ordering. While the goal of this project is to abstain from recondite mathematical definitions, this concept is much easier to understand in such terms. A topological sort is an ordering of vertices $v_{1},v_{2},…v_{n}$ in such a way, that if there exists an edge with a tail of $v_{j}$ and a head of $v_{i}$, then $v_{j}$ comes before $v_{i}$. It’s a ordering of vertices in which the directed edges of the graph always move forward in the ordering. Consider a graph in which the vertices represent tasks and directed edges represent precedence constraints. The topological orderings are acceptable sequences in which to complete the tasks. This is depicted graphically below.

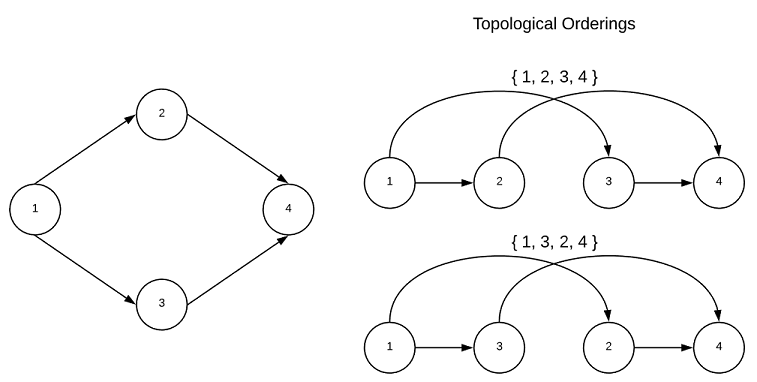
Every directed acyclic graph has a source vertex, that is a vertex with no incoming edges. Additionally, there must exists a vertex with no outgoing edges known as the sink vertex. The interested reader is encouraged to contemplate why this is true…