Deciphering connected components in a directed graph is a bit more difficult than it is in undirected graphs. A strongly connected component is a subsection of a directed graph in which there is a directed path from every vertex to every other vertex. The rather convoluted graph below demonstrates the concept.

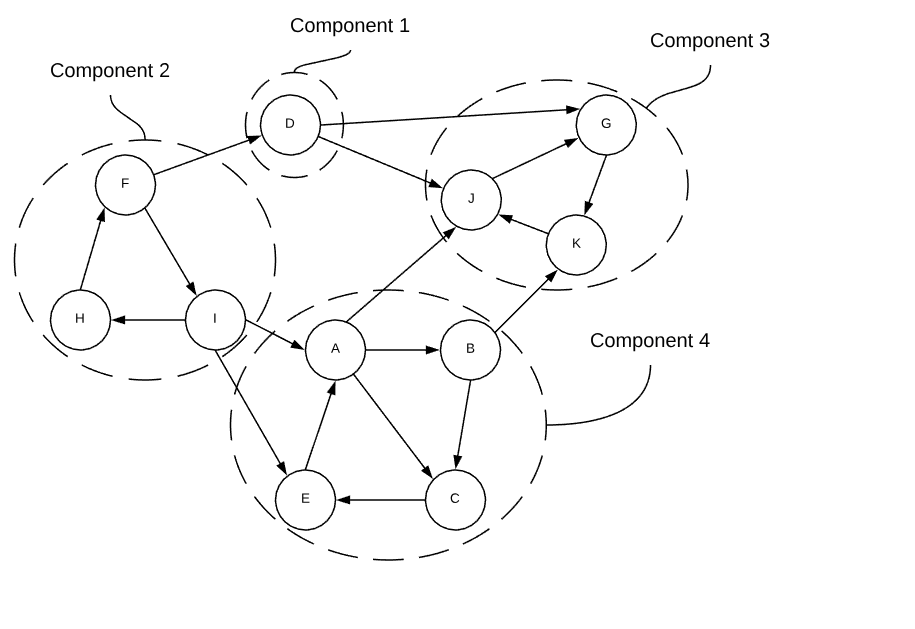
If each strongly connected component is treated as a single node, the graph becomes a directed acyclic graph. Just like nodes in a directed graph, a strongly connected components with no incoming edges is known as a source and one without any outgoing edges is known as a sink.