The minimum cut is the grouping of vertices into two non-empty groups having the fewest number of crossing edges. Consider the graph in the graphic below. There is no other way of dividing the vertices that would result in fewer crossing edges.

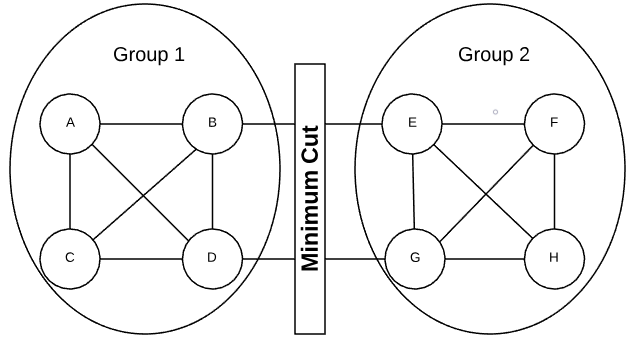
In an undirected graph, a crossing edge is considered any edge that has an end point in both groups. A crossing edge in a directed graph is when an edge has a tail in group 1 and a head in group 2. The minimum cut size is the number of crossing edges. Logically, the size cannot exceed the minimum degree of the graph.