Conceptually, an Independent Set (IS) is comparable to the inverse of a graph. It’s a set of vertices that do not contain both endpoints of any edge. Consider a connected graph with only three vertices as shown below. There are five independent sets.

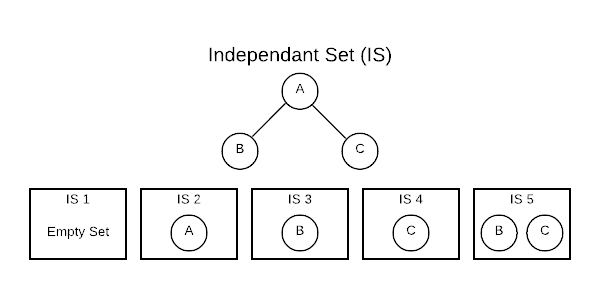
The [] (empty set) is always considered an IS because it technically fits the definition. The sets [A], [B], and [C] are also ISs because no edge contains only one vertex. The set [B, C] also qualifies because there are no edges connecting B and C. One important thing to note is that the number of ISs grows exponentially as the number of vertices grow. This has important algorithmic implications.

At first glance, this concept seems a bit academic; however, ISs are useful in practice. Finding an IS is a way of asking, which vertices do not have a relationship. For instance, if vertices are people and edges are familial relationship, an IS would define people who are not related.