Johnson's Shortest Path

• Reduces the all pairs shortest path problem to $n$ iterations of Dijkstra’s algorithm while accommodating negative edge lengths.
• Reduces to:
  • 1 invocation of Bellman-Ford
  • $n$ invocations of Dijkstra’s

Suppose $G=(V,E)$ is a directed graph with edge lengths. Obtain $G^\prime$ from $G$ by adding a constant $M$ to every edge length. The shortest path between a source $s$ and a destination $t$ is guaranteed to be the same in $G$ and $G^\prime$ when all $s-t$ paths of $G$ have the same number of edges.

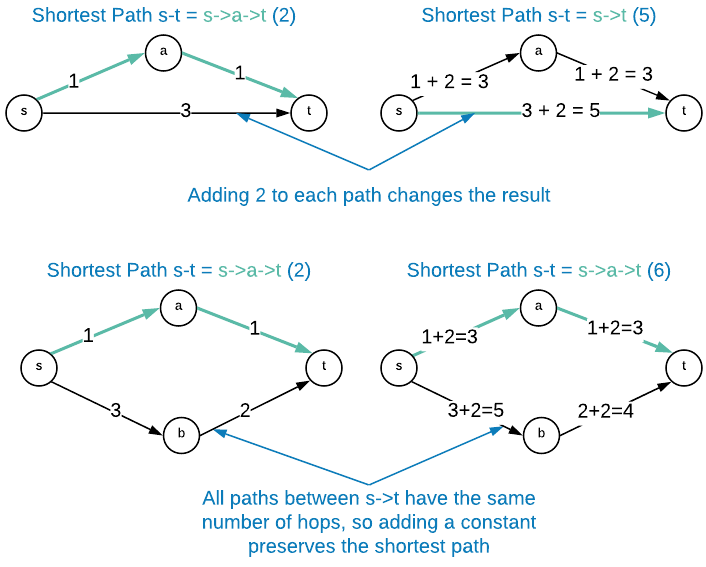
Steps:

1. Add a new vertex ($S$) to graph with a zero weight edge to every existing vertex. This ensure that every vertex is reachable from a source vertex.
2. Compute the shortest path from $S$ to every other vertex using the Bellman-Ford algorithm.
   • If a negative cycle exists, report and quit
3. Re-weight the vertices using $e_w = e_w + P_u - P_v$
   • $e_w$ = edge weight
   • $P_u$ = shortest path calculation for tail
   • $P_v$ = shortest path calculation for head
4. Run Dijkstra’s algorithm for every $v \in V$
5. Restore the original weights by using $e_w = e_w - P_u + P_v$

Applications

• List of commonly used application

Asymptotic Complexity

\(O(nm\log_2{n})\)

Pseudo Code

inputs:
    input 1
    input 2

side effect(s):
    effect 1
    effect 2

returns:
    some value

invariants:
    1 = 1

// intialize variables

function:
    code here

code goes in here

Source Code

Full Repo

Relevant Files:

• File.h
• File.c
• FileTest.c

Click here for build and run instructions