Dijkstra’s shortest path algorithm calculates the shortest distance between vertices in a weighted graph with non-negative edge weights. This is without a doubt one of the greatest hits of algorithms with countless applications. Those wishing to excel in computer science should take extra car to ensure they fully understand this.
A common error is to assume that the non-negative edge weight constraint is circumventable by increasing the value of each edge weight by the absolute value of the smallest edge weight ($\mid\min{e_w\in E}\mid$). The flaw in this assumption is best demonstrated with an example.
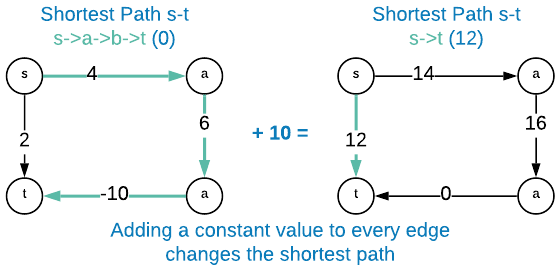
As the graphic above illustrates, adding a constant value to each edge weight results in altering the shortest path.
The algorithm as shown in the this section is a naive implementation. Each iteration of the main while loop requires a scan over all edges to find the one with the minimum distance. While this runtime isn’t horrible, it’s possible to do much better using the implementation in the next section.
Asymptotic Complexity
$O(mn)$
Pseudo Code
dijkstra:
G = input graph with distance of each vertex set to infinity
v = starting vertex
side effects: marks all vertices with the shortest distance from the starting
vertex
S = empty array
v.distance = 0
S.add(v)
while true:
u = find_min(G, S)
if u is NULL or u.distance == infinity:
break
S.add(u)
find_min:
G = input graph
S = array containing all conquered vertices
v = NULL
for each vertex in S:
for each edge in vertex:
if edge.head is contained in S:
continue
distance = edge.tail.distance + edge.weight
if distance < edge.head.distance
edge.head.distance = distance
if edge.head.distance < v.distance
v = edge.head
return v
Source Code
Relevant Files:
Click here for build and run instructions