Deciphering connected components in a directed graph is a bit more difficult than it is in undirected graphs. A strongly connected component is a subsection of a directed graph in which there is a directed path from every vertex to every other vertex. The rather convoluted graph below demonstrates the concept.
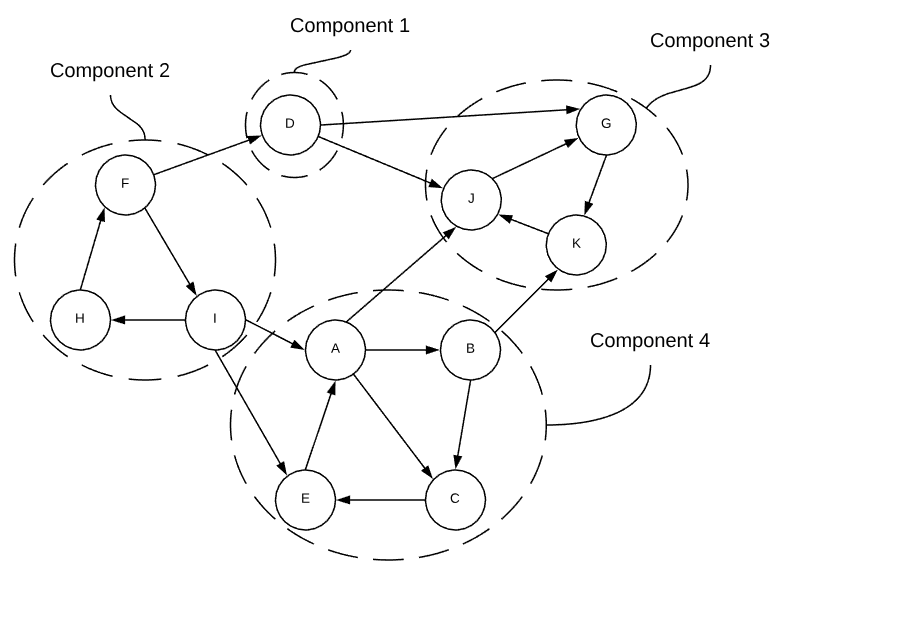
If each strongly connected component is treated as a single node, the graph becomes a directed acyclic graph. Just like nodes in a directed graph, a strongly connected components with no incoming edges is known as a source and one without any outgoing edges is known as a sink.
Finding the strongly connected components of a directed graph is the most complex of the algorithms shown here. This algorithm (often referred to as the Kosaraju or Kosaraju-Sharir algorithm) performs DFS twice. The first time it derives an ordering in which to process the vertices that guarantees the second pass of DFS will start with a sink component. In other words, the goal is to identify the reverse topological ordering of all strongly connected components. The second discovers the strongly connected components.
Applications
- Collapse a complicated graph into a more manageable graph.
Asymptotic Complexity
\(O(m + n)\)
Pseudo Code
strong-connected-components:
G = input graph
S = stack to hold ordering
magic-ordering(G, S)
set all vertices to NOT conquered
while S is not empty:
v = S->pop
if v is NOT conquered:
scc-dfs(G, v)
scc-dfs:
G = input graph
v = starting vertex
scc_id = strongly connected component id to mark all vertices with
side effects: marks all reachable vertices with a strongly connected
component id
s = new stack data structure
s->push(v)
while s is not empty:
v = s->pop
if v is NOT conquered:
conquer(v)
v->scc_id = scc_id
for each edge in v:
w = edge->head
s->push(w)
// equivalent to a topological sort with the direction of the edges reversed
magic-ordering:
G = input graph
S = stack to hold ordering
for every vertex in G:
if vertex is NOT conquered:
reverse-topo-sort(G, S, vertex)
reverse-topo-sort:
G = input graph
S = stack to hold ordering
v = starting vertex
side effect: places vertices on the stack in the "magic order"
conquer(v)
for each incoming edge in V:
w = edge->tail
if w is NOT conquered:
reverse-topo-sort(G, S, w)
S->push(v)
Source Code
Relevant Files:
Click here for build and run instructions