Welcome to the second installment of this three-part series on coding theory. If you have not had the opportunity to read the first piece, it is highly recommended that you do before continuing on. It is available here: Coding Theory (Part 1 of 3) - Coding Theory Defined
It’s rare to find concepts simple yet adroit at the same time. However, Hamming’s contributions to coding theory “fits the bill”. This post begins with a brief introduction to Hamming and a short history lesson before diving into Hamming Distance, and Perfect Codes. Additionally, it delves into a few simple math concepts requisite for understanding the final post. These concepts all come together in the final installment by providing examples of how to generate and decode the most powerful and efficient error correcting codes in use today.
Richard Hamming
Richard Hamming was an American mathematician that lived from 1915 thru 1998. Early in his career, he programmed IBM calculating machines for the infamous Manhattan project. Concerned about the pernicious effect he may be having on humanity, he abandoned the Manhattan project to work for Bell Laboratories in 1946. Hamming’s tenure at Bell Laboratories was illustrious. His contributions during that time include Hamming codes, Hamming matrix, Hamming window, Hamming numbers, Hamming bound, and Hamming distance. The impact of these discoveries had irrevocable implications on the fields of computer science and telecommunications. After leaving Bell Laboratories in 1976, Hamming went into academia until his death in 1998.
The Inception of Error Correcting Codes
The world of computation was very different back in 1947. At that time, producing modest (by today’s standards) calculations could take days. Just like today, machines of yore operated on bit strings with parity bits to ensure data fidelity. However, upon detecting erroneous data, the machines had no choice but to halt computation and return an error result. Imagine the frustration of being 47 hours into a 48-hour program and having it error out due to an anomaly introduced by noise. This is the dilemma Richard Hamming faced.
In 1950, Hamming published a paper that would serve as the basis for modern coding theory. He postulated that it was possible to not only detect, but correct errors in bit strings by calculating the number of bits disparate between valid codes and the erroneous code. This came to be known as Hamming Distance.
Hamming Distance
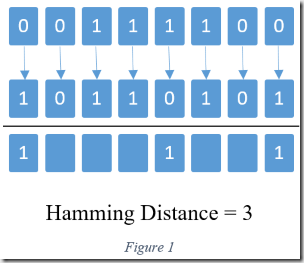
The Hamming distance between two codewords is simply the number of bits that are disparate between two bit strings as demonstrated in figure one. Typically, hamming distance is denoted by the function \(d(x,y)\) where \(x\) and \(y\) are codewords. This concept seems incredibly mundane on the surface, but it’s the inception of a whole new paradigm in error correcting codes; specifically, Nearest Neighbor error correction.
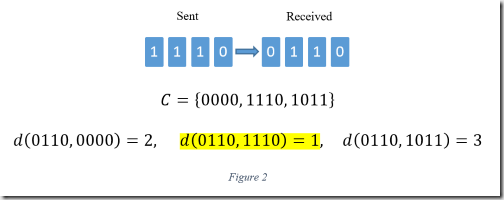
Nearest neighbor error correction involves first defining codewords, typically denoted as \(C\), that are known to both the source and sink. Any received codeword not contained in \(C\) is obviously the result of noise. Upon identifying an erroneous codeword, nearest neighbor decoding calculates the Hamming distance between it and every codeword contained in \(C\). The codeword with the smallest Hamming distance has a high probability of being correct. See figure two.
The quality of error correction is heavily dependent on choosing efficient codewords. \(d(C)\) denotes Minimum Hamming Distance: that is the smallest hamming distance between any two code words contained within \(C\). If a code has a minimum hamming distance of one (\(d(C)=1\)) then nearest neighbor error correction is futile. If it has a large hamming distance, such as 10 (\(d(C)=10\)), then error correction is powerful.
Hamming represented the relationship between minimum hamming distance and the quality of error correction with two concise equations. A particular code can detect a maximum \(k\) errors in a codeword if \(d(C)≤k+1\) and correct a maximum of \(k\) errors if \(d(C)≥2k+1\). For example, a code with \(d(C)=10\) can detect a maximum of nine errors and correct a maximum of four as demonstrated in figure 3.

An important fact to note is that the equations above represent the maximum bounds of error detection and correction. It is possible to create a code with a minimum hamming distance that falls short of these bounds. In reality, it’s difficult to create a code that effectuates the bounds. There are special codes, known as Perfect Codes, that meet this criterion as well as demonstrate some other desirable traits.
Perfect Codes
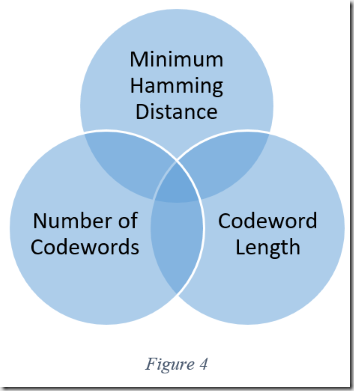
Generating an efficient code is a formidable task because it involves three competing principals as shown in figure four. First, short codewords reduce the size of data transmissions. Likewise, as shown in the previous section, the greater the minimum Hamming distance, the greater the codes ability to detect and correct errors. However, there are a limited number of codewords of a specified length that also have a specified minimum Hamming distance.
The Hamming Bound equation demonstrates these competing principals concisely. The equation is shown in figure five, where \(|C|\) is the upper bound number of codewords, \(n\) is the length of the codewords, and \(k\) is the maximum number of errors it is capable of correcting. Any code that achieves the upper bound of the equation is known as a Perfect Code. As a side note, Richard Hamming developed a perfect code known now as Hamming Codes.

Conclusion
This concludes the second installment of this three-part series on coding theory. Richard Hamming created error correcting codes that addressed the problem of brittle computations in the 1950s. However, they still permeate modern computer science. The concept of Hamming Distance incepted Nearest Neighbor error correction. The quality of error correction is dependent on the Hamming Bound, which is an equation that expresses the three competing goals of an effective code.
Make sure to check back for the final installment of this series. To date, the posts have covered mostly supporting concepts. However, the concluding piece agglomerates all ideas into a cohesive whole with an example. As always, thank you for reading and feel free to contact me with questions or comments.