Coding theory stands as a cornerstone for most of computer science. However, many programmers today have a diminutive understanding of the field at best. This three-part series of blog posts describes what coding theory is and delves into Richard Hamming’s contributions. Although derived in the 1950s, Hamming’s ideas are so visionary that they still permeate modern coding applications. If a person truly comprehends Hamming’s work, they can fully appreciate coding theory and its significance to computer science.
This first installment of the series defines coding theory, error detecting codes, and error correcting codes. These are all important supporting concepts required to fully appreciate future articles. Although this is aimed at the novice, it will provide a good review for the more seasoned computer scientist.
Coding Theory Defined
Computer systems store information as a series of bits. Coding theory is the study of encoding, transmitting, and decoding said information in a reliable manner. More succinctly: moving bits with fidelity. This appears elementary from the cursory view. What’s difficult about transferring ones and zeros across some communications medium? As figure one illustrates, the answer is the noise introduced by the communications channel.

Recall that computer systems store data as a strings of bits. Each bit has two possible values. These values are often represented as 1/0, true/false, on/off, or even high/low. Regardless of the nomenclature used to represent them, they are nothing more than the absence or presence of a voltage from a computer’s perspective. Noise, including everything from electrical interference to a scratched disk surface, can make these values ambiguous to a machine.
As a grossly simplified example, suppose a computer expects either a zero or five-volt signal. A zero-volt signal goes into one side of the channel and distortion causes 2.6 volts to come out the other side. Therein lies the ambiguity. The machine can only interpret the signal as a one and rely on coding techniques to sort it out.
One important point to remember is that coding theory is requisite due to shortcomings in modern computer hardware. If contemporary machines could transmit data reliably, coding theory would be superfluous. It’s not that building such equipment is impossible. The technology to build reliable machines exists. It’s just not practical. Such computers would be slow and exorbitantly expensive. Richard Hamming stated: “We use coding theory to escape the necessity of doing things right because it’s too expensive to do it right” (Source).
Coding theory addresses the inadequacies of machines by building fault tolerance directly into transmitted data in the form of error detecting and error correcting codes.
Error Detecting Codes
Aptly named, error detecting codes enable receivers to determine if accepted information contains errors. This is possible by appending calculated verification data to the data source before transmission. The sender calculates verification data by running the source data through a deterministic algorithm which typically produces either a hash, checksum, or parity bit. Upon receipt, the receiver runs the same algorithm on the information received. If the data produced by the receiver matches the verification data, it’s safe to assume the accepted information is unadulterated. Figure two shows the process more concisely.
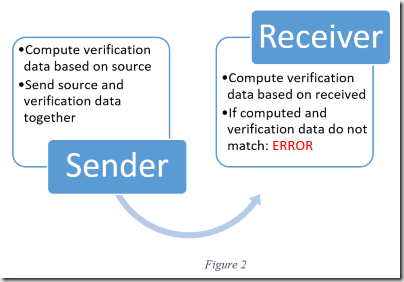
The concept of using codes for error detection is actually quite old. Scribes in antiquity would sum the number of words in paragraphs and pages and use those values to detect transcription errors. In that case, the original scroll is the source and the produced scroll is the sink. The scribe himself is the communication channel and source of noise. The algorithm used to generate the verification data is the process of counting the words. Obviously, error detecting is more complex in modern times but the general principal remains unchanged.
Error detection goes beyond simply detecting errors introduced by noise; it can also detect information tampering by malicious third parties. Although fascinating, all of that minutiae is beyond the scope of this post. For brevity, this article explores the simplest type of error detecting codes: parity bits. This is the only error coding concept particularly germane to future installments in this series.
A parity bit (aka check bit) is a verification bit appended to the end of a codeword. The parity bit equals zero if there are an even number of ones and one if there are an odd number. Figure 3 illustrates this concept. As a side note, what is described above is technically an “even” parity bit. The bit value will be the opposite in the case of an odd parity bit. The remainder of this article assumes even parity bits.

Parity bits can only detect an odd number of errors. Consider the seven bit codewords above. The parity bit is only useful if there are one, three, five, or seven errors. If there are two, four, or six error, the parity bit indicates success. One method for mitigating this is by arranging the data into a matrix and generating parity bits in multiple dimensions as shown in figure four.
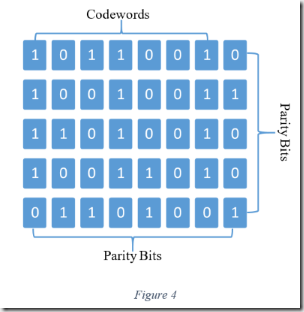
The example shown above has two dimensions; however, it’s possible to add parity bits in unlimited dimensions. While it’s fairly easy to imagine a matrix with three dimensions, it’s arduous to visualize a matrix with more than that. Regardless, it’s mathematically feasible. A future article in this series examines this in more detail.
Error detecting codes inform the receiver of errors during the transmission of information. Knowing there is an error, the receivers can easily make a request to resend data. Many systems work exactly like this. The next section explores how coding theory takes this one step farther by not only detecting errors, but correcting them as well.
Error Correcting Codes
The previous section describes how receivers request a resend upon detecting errors with error detecting codes. Unfortunately, there are applications where this isn’t an option. For instance, imagine trying to communicate with a satellite in deep space when the transmission process could take months. Another example is data stored on a disk that may degrade over time. It’s impossible to ask for a retransmission from the source because the source itself is corrupted. Yet another example is broadcast systems where there is no backchannel to facilitate resend requests. These are just a few examples. For such cases there are error correcting codes which not only inform the receiver of errors, they contain enough information to fix them.
The simplest form of error correcting codes are repetition codes. As the name implies, the message is simply replicated multiple times. The decoder determines the correct bits by choosing the majority. Figure five illustrates the concept. The amount of duplication is implementation dependent; however, less than thrice is not effective.

There are more elegant and efficient error correction paradigms than repetition codes. However, they are still in use in some modern system due to the ease of implementation. The main take away from this section is simply what error correcting codes are. Future installments examine them in greater detail.
Conclusion
This concludes the first installment of this three-part series on coding theory. This article introduced coding theory, error detecting codes, and error correcting codes. In short, the concepts required to fully appreciate future posts. Future installments dig into details of coding theory and explore the works of Richard Hamming, who revolutionized the field in the 1950s.
Make sure to come back for the next article because that’s when things start to get exciting. The post digs into some fascinating math and the more ingenious methods used for error correction. As always, thank you for reading and feel free to contact me with questions or comments.