How Woodland Creatures Broke Computation

Consider this ostensibly innocuous number sequence:

\[[1, 6, 21, 107, ...]\]

Take a few minutes and try to divine the 5th number.

Don’t feel bad if it’s not immediately apparent; you’re looking at the Busy Beaver sequence¹. The 5^th, and all subsequent numbers, have eluded the world’s best and brightest mathematicians and computer scientists since its inception. The mystery is rooted in the growth rate: it progresses so fast that no computable function can keep up with it. Follow along for a fascinating foray into the limits of computability.

The concepts presented here depend upon the Turing Machine model of computation and the Halting Problem. Please see this previous blog post for an introduction to the topics if you are unfamiliar.

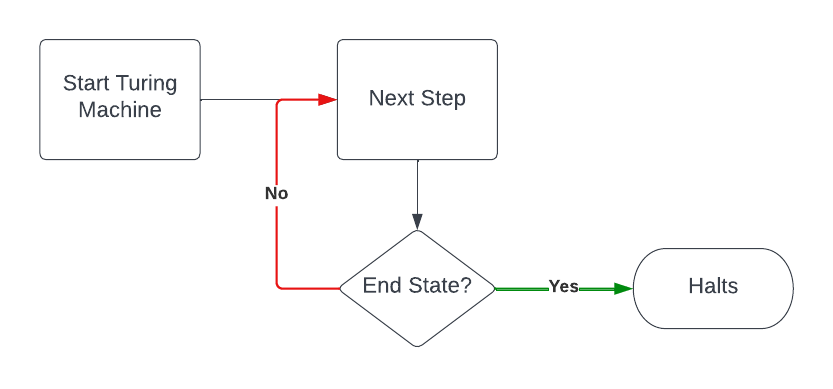
The Busy Beaver sequence originates from Tibor Radó’s brilliant ² 1962 paper On Non-Computable Functions. It’s an attempt to circumvent the Halting Problem³, which asserts that no Turing machine can determine if a given Turing machine will halt or run ad infinitum. The only option is to run the machine and see if it stops; however, there’s no way of knowing if it will ever stop. It’s a theoretical brick wall that seems impassable. Notice the infinite loop in the algorithm shown below.

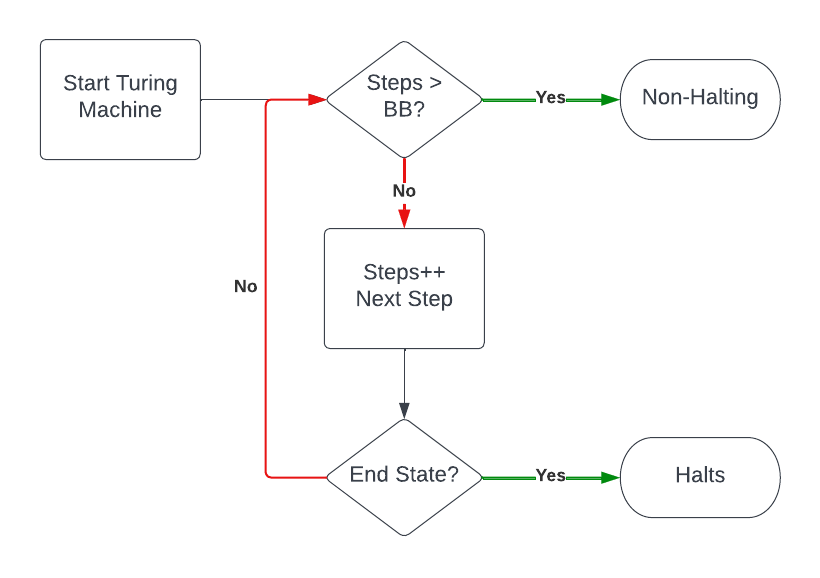
Mr. Radó considered an “outside the box” solution. What if you knew, in advance, the maximum number of steps that any halting Turing machine would execute? Envision a Turing machine as a beaver, busily completing steps, and you know the busiest beaver ($BB$) that’s not infinitely busy⁴. The halting problem is suddenly tractable, as depicted below.

$BB$ is an astonishingly high number partially because it considers all conceivable halting Turing machines. It’s possible to reduce the problem space by grouping machines by their number of rules (size)⁵. $BB$ becomes $BB(n)$ with $n$ being the size of the input machine. Once again, see the algorithm below.

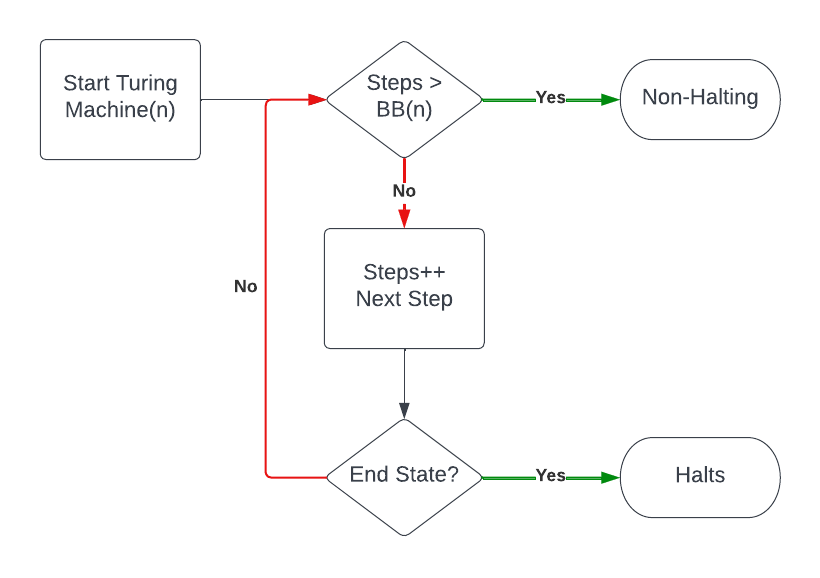
As a concrete example, consider a machine with four rules. We know from this article’s introduction that $BB(4) = 107$. The algorithm will loop no more than 107 times to determine if the input machine halts.

One might wonder why these numbers are so difficult to compute. Turing’s paper, On Computable Numbers⁶, proves it’s impossible to write an algorithm to determine $BB(n)$ because $BB(n)$ is reducible to a solution to the Halting problem. However, the fact that it’s non-computable does not mean it’s inherently unknowable. One can discover $BB(n)$ using this procedure:

1. Simulate all Turning machines of size $n$.
   • There are $[4(n+1)]^{2n}$ possible machine where $n=$size. The magnitude of possibilities alone is intractable.
2. Execute each machine.
   • Gain a small efficiency by automatically eliminating machines without a stop state.
3. Conduct a meta-analysis of each running machine to locate infinite loops.

The final step is notoriously tricky because loops may be nested billions of instructions deep. While not impossible, it’s undoubtedly intractable, manual, and tedious.

Things may seem a bit benign till now, but it’s about to get mind-blowing. The introduction mentions that $BB(5)$ and above are unknown. That’s a bit of an exaggeration; it’s known that $BB(5)$ is at least as high as 47,176,870 and $BB(6)$ is at least as high as 8,690,333,381,690,951⁷. It would have been nearly impossible to have surmised $BB$’s astronomical growth rate based on the first four numbers in the sequence. How fast is the growth rate exactly? Faster than any machine can compute, even in theory.

Consider this. Suppose you could conceive a function that grows faster than $BB(n)$; let’s call it $BB(n)\prime$. Plug $BB(n)\prime$ into the flow chart above, and you’ll see it serves the same purpose. As has already been established, defining such a function is impossible. Stated differently, it’s provable that $BB(n)$ will always be larger than any computable function for sufficiently large values of $n$.

Let that sink in: $BB(n)$ grows faster than any machine could compute, even in principle. Define any function: $n^{n!}$, or $tree(n)$, absolutely anything computable. Given a sufficiently large value of $n$, $BB(n)$ produces a higher value.