The goal of this article is to provide laymen with a conceptual understanding of diagonalization. Those interested in a deep dive full of mathematical jargon will be sorely disappointed. However, this piece is the perfect resource for a general understanding of the topic devoid of the more arcane details. Unlike the majority of my writing, this is not directly applicable to the daily responsibilities of software professionals. It is purely an endeavor to satisfy intellectual curiosity.
Why?
The impetus for this writing comes from a colleague who contacted me after reading my blog series on Set Theory (Set Theory Defined, Set Operations, When Sets Collide). The posts made pithy mention of Cantor’s diagonalization proof with implications on infinite cardinality. My friend’s search for a concise explanation proved to be unfruitful. The conversation naturally progressed toward Alan Turing’s seminal paper: On Computable Numbers, which also employs a diagonalization proof. Cantor and Turing both played a major part in shaping computer science. Therefore, although it is not likely that the majority of software professionals will ever employ diagonalization, it’s a crucial part of computing history.
What Are We Trying to Prove?
Diagonalization is a mathematical proof demonstrating that there are certain numbers that cannot be enumerated. Stated differently, there are numbers that cannot be listed sequentially. Consider all the numbers on the number line as shown in Figure One – Number Line.

First consider the set of positive whole numbers including zero. These are known as natural or counting numbers and are denoted as \(\mathbb{N}\) . Most kindergarten curriculum teaches how to enumerate this set: starting with zero add one to the current number to get the next number ad infinitum.
Adding negative numbers to \(\mathbb{N}\) produces the set of integers denoted by \(\mathbb{Z}\) . Again, this set is also easy to enumerate by simply listing it as follows: \(0, 1, -1, 2, -2, 3, -3, …\)
Now consider expanding on \(\mathbb{Z}\) by adding fractions to create the set of rational number denoted as \(\mathbb{Q}\) . The term rational signifies that a number can be expressed as a ratio such as \(1/2\) or \(23/345\) . These numbers fit between the whole number on the number line and there is an infinite amount of fractional numbers between each set of natural numbers. That is to say, regardless of the location of two rationals on the number line, it’s always possible to find another number between them. With some ingenuity, these numbers can also be enumerated in several different ways. Enumerating rational numbers, while fascinating, is beyond the scope of this post. The reader is encouraged to either just accept my word as fact or do research.
Although it seems as if we’ve run out room on the number line, that isn’t actually the fact. There is another class of number that has been baffling mathematicians throughout the ages: irrational. It’s a bit perplexing, but irrationals fit between rationals on the number line (no matter how many times I think about that, it amazes me). Grade school curriculum typically introduces the concept with renowned numbers such as \(\pi\) or \(e\). These are numbers that cannot be expressed as a ratio. The decimal representation consists of an infinite series of digits with no repeating pattern. Any calculations involving irrationals are approximations because it’s impossible to express them in a finite context. Adding these to \(\mathbb{Q}\) produces the set of real numbers denoted as \(\mathbb{R}\). Irrational numbers are the target of our inquisition.
As a matter of note, the set of irrational numbers can be further divided into the sets of algebraic and transcendental numbers. Algebraic numbers can in fact be enumerated. However, this is a bit of minutia that isn’t really necessary for understanding diagonalization. Once again, the curious reader is encouraged to rely on Google for further inquiry.
The question is, how is it possible to prove that irrational numbers are not enumerable. With an understanding of the problem, we can turn our attention to the solution which is diagonalization.
Reductio Ad Absurdum
Diagonalization is a type of proof known as reductio ad absurdum which is Latin for reduction to absurdity. It is common amongst mathematicians and philosophers alike. The premise is to first assume a proposition is true and then disprove it via deductive reasoning thus reducing it to an absurd conclusion.
One popular example of a reductio ad absurdum proof is that there is no smallest fractional number. Assume there is such a number: it can be divided by two to create a smaller number. Therefore, the original assumption is absurd. Another illustration is an alibi. First assume the suspect committed the crime. If the accused is known to be at a different location when the crime took place, it’s absurd to assume that they were also at the scene of the crime.
Diagonalization
Having addressed all the introductory trivialities, it’s time to get to the point. The diagonalization proof is as follows. First assume that it is possible to enumerate all irrational numbers. If this is true, it should be impossible to devise a number that is not included in this list. Examine Figure Two – Diagonalization and stretch the mind to imagine that this is in fact the list of all irrational numbers: the list is infinitely long and each number expands on endlessly. Next, draw a diagonal line down the center of the list and write down the resulting infinite number. In this case, the number is \(0.13579135…\). Next add 1 to each digit expect in the case of nine which becomes a zero. This results is the number \(0.24680246…\). Is this number contained in the list? It’s obviously not the first number because the first digit does not match. The same holds true for the second number because the second digit has to be different. Continue this line of logic for every number and it’s obvious that the devised number is not in the list. The reader should take a few minutes to let that sink in.
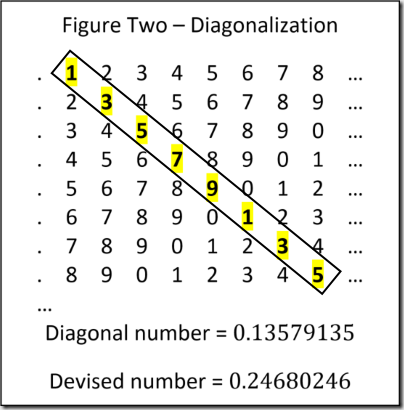
Keep in mind, this is purely a thought experiment. Obviously, Figure Two – Diagonalization is not an infinite list and each number is not truly irrational. It’s impossible to construct such a list in a finite context. However, the line of logic holds true.
It is common to wonder why diagonalization does not apply to \(\mathbb{Q}\). The concise answer is that those numbers have finite digits and irrationals do not.
Implications
Accepting that the diagonalization proof is valid, it has some profound implications. At first glance, it’s difficult to understand how the fact that it’s impossible to enumerate irrational numbers has bearing on the world in any way. However, many people have derived some amazing conclusions. Cantor showed that there are in fact multiple infinities. Turing used diagonalization to prove the limits of computability. It’s even been employed by philosophers to prove that there are an insufficient number of proofs to prove all the truths in the universe. More concisely, some truths are unproveable. The implications lead down an exceedingly dark and deep rabbit hole.
Conclusion
Diagonalization is a reductio ad absurdum proof that demonstrates the impossibility of enumerating irrational numbers. It is relatively easy for non-mathematicians to understand. While only tangentially related to software engineering, it’s a fascinating concept that sheds light on the foundations of computing and indeed the world.
As always, thank you for taking the time to read this article. Please feel free to contact me with any questions or concerns.